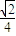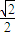题目内容
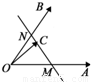
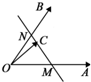
如图所示,两个非共线向量 ,
, 的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且
的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且 =x
=x +y
+y (x,y∈R),则x2+y2的最小值为( )
(x,y∈R),则x2+y2的最小值为( )
A.

B.

C.

D.

【答案】分析:法一:特殊值法,当θ=90°,|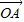 |=|
|=|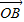 |=1时,建立直角坐标系,得x+y=
|=1时,建立直角坐标系,得x+y= ,所以x2+y2的最小值为原点到直线的距离的平方;
,所以x2+y2的最小值为原点到直线的距离的平方;
解法二:因为点C、M、N共线,所以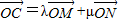 ,有λ+μ=1,由M、N分别为OA与OB的中点,可得x+y=
,有λ+μ=1,由M、N分别为OA与OB的中点,可得x+y=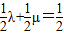 ,下同法一
,下同法一
解答: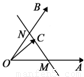 解法一:特殊值法,当θ=90°,|
解法一:特殊值法,当θ=90°,|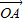 |=|
|=|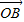 |=1时,建立直角坐标系,
|=1时,建立直角坐标系,
∴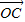 =x
=x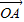 +y
+y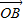
得x+y= ,所以x2+y2的最小值为原点到直线的距离的平方;
,所以x2+y2的最小值为原点到直线的距离的平方;
解法二:因为点C、M、N共线,所以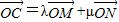 ,有λ+μ=1,
,有λ+μ=1,
又因为M、N分别为OA与OB的中点,
所以 =
=
∴x+y=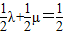
原题转化为:当x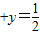 时,求x2+y2的最小值问题,
时,求x2+y2的最小值问题,
∵y=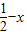
∴x2+y2= =
=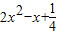
结合二次函数的性质可知,当x= 时,取得最小值为
时,取得最小值为
故选B
点评:本题主要考查了平面向量的应用,解题的关键是向量共线定理的应用及结论“点C、M、N共线,所以 ,有λ+μ=1“的应用
,有λ+μ=1“的应用
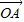 |=|
|=|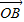 |=1时,建立直角坐标系,得x+y=
|=1时,建立直角坐标系,得x+y= ,所以x2+y2的最小值为原点到直线的距离的平方;
,所以x2+y2的最小值为原点到直线的距离的平方;解法二:因为点C、M、N共线,所以
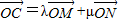 ,有λ+μ=1,由M、N分别为OA与OB的中点,可得x+y=
,有λ+μ=1,由M、N分别为OA与OB的中点,可得x+y=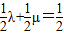 ,下同法一
,下同法一解答:
 解法一:特殊值法,当θ=90°,|
解法一:特殊值法,当θ=90°,|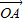 |=|
|=|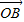 |=1时,建立直角坐标系,
|=1时,建立直角坐标系,∴
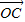 =x
=x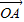 +y
+y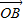
得x+y=
 ,所以x2+y2的最小值为原点到直线的距离的平方;
,所以x2+y2的最小值为原点到直线的距离的平方;解法二:因为点C、M、N共线,所以
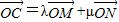 ,有λ+μ=1,
,有λ+μ=1,又因为M、N分别为OA与OB的中点,
所以
 =
=
∴x+y=
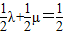
原题转化为:当x
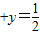 时,求x2+y2的最小值问题,
时,求x2+y2的最小值问题,∵y=
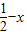
∴x2+y2=
 =
=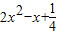
结合二次函数的性质可知,当x=
 时,取得最小值为
时,取得最小值为
故选B
点评:本题主要考查了平面向量的应用,解题的关键是向量共线定理的应用及结论“点C、M、N共线,所以
 ,有λ+μ=1“的应用
,有λ+μ=1“的应用 
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 如图所示,两个非共线向量
如图所示,两个非共线向量
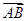 相等的向量共有几个;
相等的向量共有几个;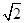 的向量共有几个?
的向量共有几个? 如图所示,两个非共线向量
如图所示,两个非共线向量 ,
, 的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且
的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且 =x
=x



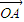 ,
,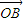 的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且
的夹角为θ,M、N分别为OA与OB的中点,点C在直线MN上,且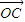 =x
=x +y
+y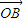 (x,y∈R),则x2+y2的最小值为( )
(x,y∈R),则x2+y2的最小值为( )