题目内容
函数f(x)=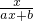 (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解.
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解.
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立?为什么?
(3)在直角坐标系中,求定点A(-3,1)到此函数图象上任意一点P的距离|AP|的最小值.
解:(1)由f(2)=1得2a+b=2,又x=0一定是方程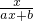 =x的解,
=x的解,
所以 =1无解或有解为0,(3分)
=1无解或有解为0,(3分)
若无解,则ax+b=1无解,得a=0,矛盾,
若有解为0,则b=1,所以a= . (6分)
. (6分)
(2)f(x)= ,设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,
,设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,
取x=0,则f(0)+f(m-0)=4,即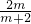 =4,m=-4(必要性)(8分)
=4,m=-4(必要性)(8分)
又m=-4时,f(x)+f(-4-x)=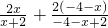 =…=4成立(充分性) (10分)
=…=4成立(充分性) (10分)
所以存在常数m=-4,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,(11分)
(3)|AP|2=(x+3)2+(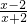 )2,设x+2=t,t≠0,(13分)
)2,设x+2=t,t≠0,(13分)
则|AP|2=(t+1)2+(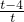 )2=t2+2t+2-
)2=t2+2t+2-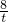 +
+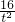 =(t2+
=(t2+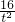 )+2(t-
)+2(t- )+2=(t-
)+2=(t- )2+2(t-
)2+2(t- )+10
)+10
=( t- +1)2+9,(16分)
+1)2+9,(16分)
所以当t- +1=0时即t=
+1=0时即t=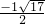 ,也就是x=
,也就是x=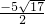 时,
时,
|AP|min=3 (18分)
分析:(1)根据方程f(x)=x,可知x=0一定是方程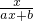 =x的解,从而有方程
=x的解,从而有方程 =1无解或有解为0,再进行分类讨论,可求a、b的值;
=1无解或有解为0,再进行分类讨论,可求a、b的值;
(2)由(1)知f(x)= ,假设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,赋值x=0,,可求参数m的值,再验证此时等式恒成立即可;
,假设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,赋值x=0,,可求参数m的值,再验证此时等式恒成立即可;
(3)先表示出|AP|2,再利用换元法,求解时整体考虑,利用配方法求解
点评:本题的考点是恒成立问题,主要考查方程解的问题,考查利用赋值法求解恒成立问题,考查函数的最值问题,关键是审清题意,合理转化,注意赋值法求解恒成立问题时,应需要验证其恒成立.
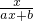 =x的解,
=x的解,所以
 =1无解或有解为0,(3分)
=1无解或有解为0,(3分)若无解,则ax+b=1无解,得a=0,矛盾,
若有解为0,则b=1,所以a=
 . (6分)
. (6分)(2)f(x)=
 ,设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,
,设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,取x=0,则f(0)+f(m-0)=4,即
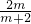 =4,m=-4(必要性)(8分)
=4,m=-4(必要性)(8分)又m=-4时,f(x)+f(-4-x)=
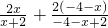 =…=4成立(充分性) (10分)
=…=4成立(充分性) (10分)所以存在常数m=-4,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,(11分)
(3)|AP|2=(x+3)2+(
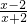 )2,设x+2=t,t≠0,(13分)
)2,设x+2=t,t≠0,(13分)则|AP|2=(t+1)2+(
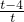 )2=t2+2t+2-
)2=t2+2t+2-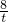 +
+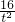 =(t2+
=(t2+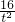 )+2(t-
)+2(t- )+2=(t-
)+2=(t- )2+2(t-
)2+2(t- )+10
)+10=( t-
 +1)2+9,(16分)
+1)2+9,(16分)所以当t-
 +1=0时即t=
+1=0时即t=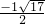 ,也就是x=
,也就是x=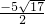 时,
时,|AP|min=3 (18分)
分析:(1)根据方程f(x)=x,可知x=0一定是方程
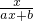 =x的解,从而有方程
=x的解,从而有方程 =1无解或有解为0,再进行分类讨论,可求a、b的值;
=1无解或有解为0,再进行分类讨论,可求a、b的值;(2)由(1)知f(x)=
 ,假设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,赋值x=0,,可求参数m的值,再验证此时等式恒成立即可;
,假设存在常数m,使得对定义域中任意的x,f(x)+f(m-x)=4恒成立,赋值x=0,,可求参数m的值,再验证此时等式恒成立即可;(3)先表示出|AP|2,再利用换元法,求解时整体考虑,利用配方法求解
点评:本题的考点是恒成立问题,主要考查方程解的问题,考查利用赋值法求解恒成立问题,考查函数的最值问题,关键是审清题意,合理转化,注意赋值法求解恒成立问题时,应需要验证其恒成立.

练习册系列答案
相关题目
已知函数f(x)=ax(a>0且a≠1)在区间[-2,2]上的值不大于2,则函数g(a)=log2a的值域是( )
A、[-
| ||||
B、(-∞,-
| ||||
C、[-
| ||||
D、[-
|
如果函数f(x)=ax2+(a+3)x-1在区间(-∞,1)上为递增的,则a的取值范围是( )
| A、[-1,0) | B、(-1,0] | C、(-1,0) | D、[-1,0] |