题目内容
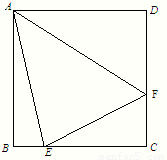
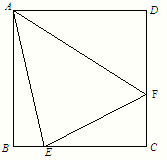 如图,开发商欲对边长为1km的正方形ABCD地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路EF(点E、F分别在BC、CD上),根据规划要求△ECF的周长为2km.
如图,开发商欲对边长为1km的正方形ABCD地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路EF(点E、F分别在BC、CD上),根据规划要求△ECF的周长为2km.(1)设∠BAE=α,∠DAF=β,试求α+β的大小;
(2)欲使△EAF的面积最小,试确定点E、F的位置.
分析:(1)根据规划要求△ECF的周长为2km,建立等式,再利用和角的正切公式,即可求得α+β的大小;
(2)先表示三角形的面积,再利用三角函数求面积的最值,从而可确定点E、F的位置.
(2)先表示三角形的面积,再利用三角函数求面积的最值,从而可确定点E、F的位置.
解答:解:(1)设CE=x,CF=y(0<x≤1,0<y≤1),则tanα=1-x,tanβ=1-y,
由已知得:x+y+
=2,即2(x+y)-xy=2…(4分)
∴tan(α+β)=
=
=1
∵0<α+β<
,∴α+β=
;…(8分)
(2)由(1)知,S△EAF=
AE×AF×sin∠EAF=
AE×AF=
×
=
×
=
=
…(12分)
∵0<α<
,∴2α+
=
,即α=
时,△EAF的面积最小,最小面积为
-1.
∵tan
=
,∴tan
=
-1,故此时BE=DF=
-1.
所以,当BE=DF=
-1时,△EAF的面积最小.…(15分)
由已知得:x+y+
| x2+y2 |
∴tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
| 2-(x+y) |
| x+y-xy |
∵0<α+β<
| π |
| 2 |
| π |
| 4 |
(2)由(1)知,S△EAF=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| 1 |
| cosαcosβ |
| ||
| 4 |
| 1 | ||
cosαcos(
|
=
| 1 |
| sin2α+2cos2α |
| 1 | ||||
|
∵0<α<
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
∵tan
| π |
| 4 |
2tan
| ||
1-tan2
|
| π |
| 8 |
| 2 |
| 2 |
所以,当BE=DF=
| 2 |
点评:本题考查三角函数知识的运用,考查和角公式的运用,考查面积的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
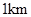 的正方形
的正方形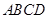 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路 (点
(点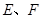 分别在
分别在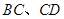 上),根据规划要求
上),根据规划要求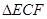 的周长为
的周长为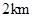 .
.
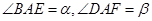 ,求证:
,求证: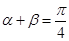 ;
;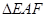 的面积最小,试确定点
的面积最小,试确定点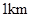 的正方形
的正方形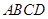 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路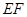 (点
(点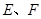 分别在
分别在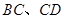 上),根据规划要求
上),根据规划要求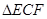 的周长为
的周长为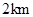 .
.
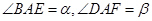 ,试求
,试求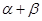 的大小;
的大小;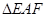 的面积最小,试确定点
的面积最小,试确定点