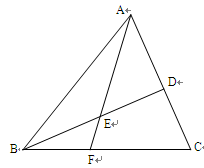
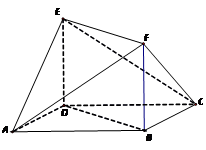
题目内容
如图,在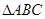 中,点
中,点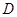 是
是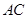 的中点,点
的中点,点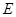 是
是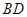 的中点,
的中点,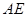 的延长线交
的延长线交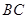 与点
与点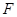 。
。
(1)求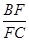 的值;
的值;
(2)若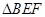 的面积为
的面积为 ,四边形
,四边形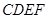 的面积为
的面积为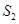 ,求
,求 的值。
的值。
(1) 
(2)根据已知条件,得到 ,同时结合
,同时结合 ,那么利用三角形面积公式来得到结论。
,那么利用三角形面积公式来得到结论。
解析试题分析:解:(I)过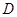 点作
点作 ,交
,交 于点
于点 。
。 点
点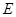 是
是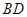 的中点,
的中点, ,又
,又
 ,则
,则 …………3分
…………3分
又 点
点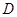 是
是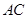 的中点,则
的中点,则
 …………5分
…………5分
(II)若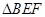 是以
是以 为底,
为底, 以
以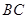 为底,则由(1)知
为底,则由(1)知
…………7分
又由 ,可知:
,可知: ,其中
,其中 分别为
分别为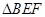 和
和 的高。
的高。
则 , 所以
, 所以
 …………10分
…………10分
考点:相似比和三角形面积的求解
点评:解决该试题的关键是利用做辅助线得到平行直线,结合平行线的性质得到比值,同时能逻辑和三角形面积公式得到结论,属于基础题。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
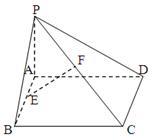
 ,
, ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使 且
且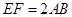 ,得一简单组合体
,得一简单组合体 如图2示,已知
如图2示,已知 分别为
分别为 的中点.
的中点.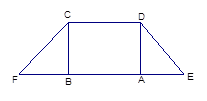

 平面
平面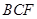 ;
;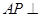
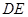 ;
;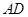 多长时,平面
多长时,平面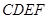 与平面
与平面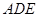 所成的锐二面角为
所成的锐二面角为 ?
?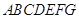 中,平面
中,平面 ∥平面
∥平面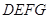 ,
,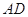 ⊥平面
⊥平面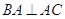 ,
,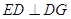 ,
,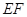 ∥
∥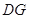 .
.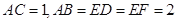 ,
, 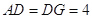 .
.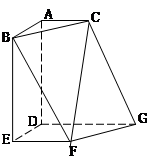
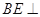 平面
平面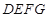 ;
;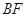 ∥平面
∥平面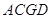 ;
;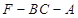 的余弦值.
的余弦值. 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点

 的平面角的余弦值.
的平面角的余弦值.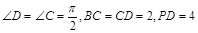 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将 沿AB折到
沿AB折到 的位置,使
的位置,使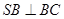 ,点E在SD上,且
,点E在SD上,且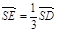 ,如下图。
,如下图。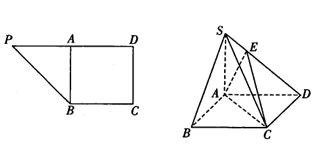
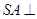 平面ABCD;
平面ABCD;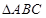 中,
中, ,
, .D、E分别是
.D、E分别是 上的点,且
上的点,且 ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.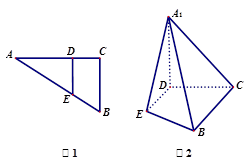
 平面
平面 ;
; ,求
,求 与平面
与平面 所成角的余弦值;
所成角的余弦值; 点在何处时,
点在何处时, 的长度最小,并求出最小值.
的长度最小,并求出最小值. 中,E为AC中点
中,E为AC中点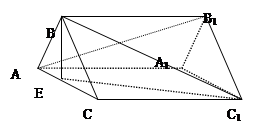

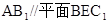 ,
, .
.
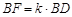 ,当二面角
,当二面角 为直二面角时,求k的值.
为直二面角时,求k的值.