题目内容
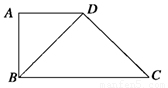
如图所示，在四边形ABCD中，EF∥BC，FG∥AD，则
=________．
1
分析：根据两条直线平行，得到平行线所截的对应线段成比例，得到两个比例式，把要求的两个比值的变化为同一条直线上的线段之间的关系，合并同类项得到一个分子和分母相等的分式，得到结果．
解答：∵EF∥BC，
∴
∵FG∥AD，
∴
，
∴=
=
故答案为：1
点评：本题考查平行线等分线段定理，考查等量代换，考查分式的整理方法，是一个基础题，这种题目是几何证明中的典型题．
分析：根据两条直线平行，得到平行线所截的对应线段成比例，得到两个比例式，把要求的两个比值的变化为同一条直线上的线段之间的关系，合并同类项得到一个分子和分母相等的分式，得到结果．
解答：∵EF∥BC，
∴
∵FG∥AD，
∴
，∴
==故答案为：1
点评：本题考查平行线等分线段定理，考查等量代换，考查分式的整理方法，是一个基础题，这种题目是几何证明中的典型题．
练习册系列答案
相关题目
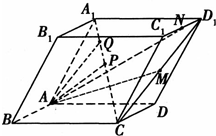如图所示，在各个面都是平行四边形的四棱柱ABCD-A1B1C1D1中，P是CA1的中点，M是CD1的中点，N是C1D1的中点，点Q在CA1上，且CQ：QA1=4：1，设
(2007
重庆，10)如图所示，在四边形ABCD中，
，
，
，
则
的值为
[
]|
A ．2 |
B ． |
C ．4 |
D ． |
