题目内容
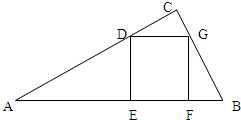
已知△ABC中,∠C=90°,D为斜边AB上靠近顶点A的三等分点.
(I)设
=
,
=
,求
;
(II)若CA=2
,CB=1,求
在
方向上的投影.
(I)设
| CA |
| a |
| CB |
| b |
| CD |
(II)若CA=2
| 2 |
| CD |
| AB |
分析:(1)由条件可得
-
=3(
-
),花简求得
=
+
.
(2)过C作CE⊥AB于E,则由射影定理得AE=
,故DE=
.再由
在
方向上的投影为负可得结果.
| CB |
| CA |
| CD |
| CA |
| CD |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
(2)过C作CE⊥AB于E,则由射影定理得AE=
| 8 |
| 3 |
| 5 |
| 3 |
| CD |
| AB |
解答:解:(1)∵
=3
,即
-
=3(
-
),…(4分)
∴3
=
+2
,又
=
,
=
,故
=
+
.…(6分)
(2)过C作CE⊥AB于E,则由射影定理得AE=
,∴DE=
.
又因为
在
方向上的投影为负,故
在
方向上的投影为-
.…(12分)
| AB |
| AD |
| CB |
| CA |
| CD |
| CA |
∴3
| CD |
| CB |
| CA |
| CA |
| a |
| CB |
| b |
| CD |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
(2)过C作CE⊥AB于E,则由射影定理得AE=
| 8 |
| 3 |
| 5 |
| 3 |
又因为
| CD |
| AB |
| CD |
| AB |
| 5 |
| 3 |
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,三角形中的几何计算,属于中档题.

练习册系列答案
相关题目
已知△ABC中,∠C=90°,直线PA⊥平面ABC,若AB=5,AC=2,则点B到平面PAC的距离为( )
A、
| ||
B、
| ||
C、2
| ||
| D、5 |
 已知△ABC中,
已知△ABC中,