题目内容
已知直角三角形ABC,其三边分为a、b、c(a>b>c).分别以三角形的a边,b边,c边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,其表面积和体积分别为S1,S2,S3和V1,V2,V3.则它们的关系为( )
| A.S1>S2>S3, V1>V2>V3 | B.S1>S2>S3, V1=V2=V3 |
| C.S1<S2<S3, V1<V2<V3 | D.S1<S2<S3, V1=V2=V3 |
C
解析试题分析:以边 所在的直线为轴旋转形成的几何体表面积为
所在的直线为轴旋转形成的几何体表面积为 ,体积
,体积 =
= ;以边
;以边 所在的直线为轴旋转形成的几何体表面积为
所在的直线为轴旋转形成的几何体表面积为 ,体积
,体积 ;以
;以 所在的直线为轴旋转形成的几何体表面积为
所在的直线为轴旋转形成的几何体表面积为 ,体积
,体积
 ,∵
,∵ ∴
∴ ,选C.
,选C.
考点:旋转体的表面积和体积.

练习册系列答案
相关题目
某几何体的三视图如下,则它的体积是( )
A.8- | B.8- | C.8-2π | D. |
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是( )
| A.8 | B. | C. | D. |
将棱长为2的正方体木块削成一个体积最大的球,则这个球的表面积为( )
A.2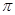 | B.4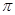 | C.8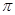 | D.16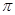 |
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
| A.84cm3 | B.92cm3 |
| C.100 cm3 | D.108cm3 |
一几何体的三视图如右所示,则该几何体的体积为( ) 
A. |
B. |
C. |
D. |
一个正四棱锥的正(主)视图如右图所示,该四棱锥侧面积和体积分别是( )
A. , , | B. , , |
C. , , | D. , , |
某几何体的三视图如图所示,则该几何体的体积是( )
A. | B. | C. | D. |
 B.
B. C. 4
C. 4 D.
D.