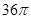题目内容
某几何体的三视图如下，则它的体积是（ ）
A．8－ | B．8－ | C．8－2π | D． |
A
解析试题分析：几何体是一个简单组合体，是一个正方体里挖去一个圆锥，边长为2的正方体，底面半径为1，高为2的圆锥，用正方体的体积减去圆锥的体积即可．
几何体是一个简单组合体，是一个正方体里挖去一个圆锥，
故选A
考点：由三视图求面积、体积．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某四棱台的三视图如图所示,则该四棱台的体积是 ( ) 
A． | B． | C． | D． |
如图为一个几何体的三视图，尺寸如图所示，则该几何体的体积为 ( )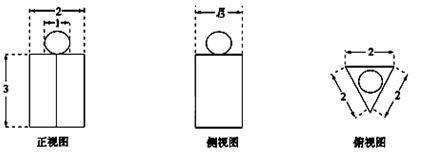
A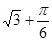． | B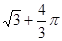． | C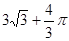． | D． |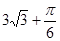
一个几何体的三视图如图，则该几何体的体积为（ ）
A． | B． |
C． | D． |
正方体的外接球与内切球的球面面积分别为S1和S2则( )
| A．S1＝2S2 | B．S1＝3S2 |
| C．S1＝4S2 | D．S1＝2 S2 |
一个几何体的三视图如图所示，正视图和侧视图都是等边三角形，且该几何体的四个点在空间直角坐标系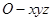
中构坐标分别是(0，0，0)，(2，0，0)，(2，2，0)，(0，2，0)，则第五个顶点的坐标可能为（ ）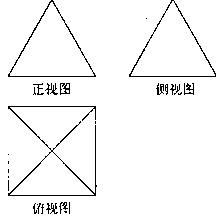
| A．（1，1，1） |
B． |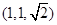
C． |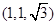
D． |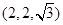
中，
、
分别是
、
的中点，且
，若侧棱
，则正三棱锥
已知直角三角形ABC,其三边分为a、b、c(a>b>c).分别以三角形的a边,b边,c边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,其表面积和体积分别为S1,S2,S3和V1,V2,V3.则它们的关系为( )
| A．S1>S2>S3, V1>V2>V3 | B．S1>S2>S3, V1=V2=V3 |
| C．S1<S2<S3, V1<V2<V3 | D．S1<S2<S3, V1=V2=V3 |