题目内容
已知在半径为4的球面上有A、 B、 C、 D四个点,且AB=CD=4,则四面体ABCD体积最大值为( )
A.  B.
B. C. 4
C. 4 D.
D.
D
解析试题分析:过CD作平面PCD,使AB⊥平面PCD,交AB于P,设P到CD的距离为h,当直径通过AB与CD的中点时, ,则有
,则有 ,故选D.
,故选D.
考点:几何体体积

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
已知直角三角形ABC,其三边分为a、b、c(a>b>c).分别以三角形的a边,b边,c边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,其表面积和体积分别为S1,S2,S3和V1,V2,V3.则它们的关系为( )
| A.S1>S2>S3, V1>V2>V3 | B.S1>S2>S3, V1=V2=V3 |
| C.S1<S2<S3, V1<V2<V3 | D.S1<S2<S3, V1=V2=V3 |
如图是一个几何体的三视图,则这个几何体的体积是 ( )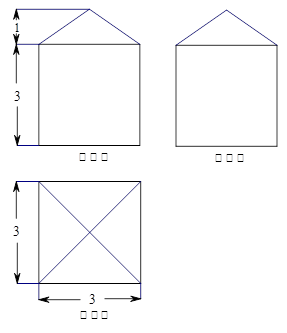
| A.27 | B.36 | C.33 | D.30 |
右图是某四棱锥的三视图,则该几何体的表面积等于( )
A. | B. |
C. | D. |
已知三棱锥 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上, 为球
为球 的直径,且
的直径,且 ,
, ,
, 为等边三角形,三棱锥
为等边三角形,三棱锥 的体积为
的体积为 ,则球
,则球 的半径为( )
的半径为( )
| A.3 | B. 1 | C.2 | D.4 |
某几何函数的三视图如图所示,则该几何的体积为( )
| A.18+8π | B.8+8π |
| C.16+16π | D.8+16π |
 中,
中, 、
、 分别是
分别是 、
、 的中点,且
的中点,且 ,若侧棱
,若侧棱 ,则正三棱锥
,则正三棱锥


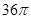

 ,球面上有A、B、C三点,如果
,球面上有A、B、C三点,如果 ,则三棱锥O-ABC 的体积为 ( )
,则三棱锥O-ABC 的体积为 ( ) (B)
(B) (C)1 (D)
(C)1 (D)
 的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( )
的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( )


