题目内容
已知正方形的中心为直线x-y+1=0和2x+y+2=0的交点,正方形的一边所在直线方程为x+3y-2=0,求其余三边方程.
分析:先由两直线的相交求出正方形的中心坐标(-1,0),然后根据所给正方形一边所在直线方程,设直线系、垂直系方程,
最后根据正方形中心到四条边距离相等求出正方形其余三边方程.
最后根据正方形中心到四条边距离相等求出正方形其余三边方程.
解答:解:因为正方形的中心为直线x-y+1=0和2x+y+2=0的交点,
所以联立方程x-y+1=0和2x+y+2=0,解方程组得:正方形中心坐标为(-1,0),
因为正方形一边所在直线方程x+3y-2=0,
所以设与之平形的另一条边所在直线方程为x+3y+m=0,与之垂直的另两条边的直线方程为3x-y+n=0,
因为中心点 (-1,0)到直线x+3y-2=0的距离为
=
,
所以
=
=
,
=
=
,
解得:m=4 或 m=-2(舍去),n=0 或 n=6.
故答案为:其余三边方程为x+3y+4=0、3x-y=0、3x-y+6=0.
所以联立方程x-y+1=0和2x+y+2=0,解方程组得:正方形中心坐标为(-1,0),
因为正方形一边所在直线方程x+3y-2=0,
所以设与之平形的另一条边所在直线方程为x+3y+m=0,与之垂直的另两条边的直线方程为3x-y+n=0,
因为中心点 (-1,0)到直线x+3y-2=0的距离为
| |-1+0-2| | ||
|
| 3 | ||
|
所以
| |-1+0+m| | ||
|
| |m-1| | ||
|
| 3 | ||
|
| |-3-0+n| | ||
|
| |n-3| | ||
|
| 3 | ||
|
解得:m=4 或 m=-2(舍去),n=0 或 n=6.
故答案为:其余三边方程为x+3y+4=0、3x-y=0、3x-y+6=0.
点评:本题主要考察平行系、垂直系方程的设法求法,属难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

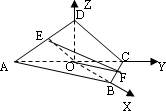
 是边长为
是边长为 的正方形
的正方形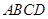 的中心,点
的中心,点 、
、 分别是
分别是 、
、 的中点,沿对角线
的中点,沿对角线 把正方形
把正方形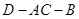 ;
;

 的大小;
的大小; 的余弦值;
的余弦值; 到面
到面 的距离.
的距离. 是边长为
是边长为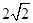 的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;