题目内容
9.函数f(x)=ln(a+x)-ln(a-x)(a>0),若曲线y=f(x)在点(0,f(0))处的切线方程为y=2x.(1)求a的值;
(2)已知x≥0时,求使f(x)≥2x+$\frac{2{x}^{3}}{3}$+M恒成立的实数M的取值范围.
分析 (1)求出原函数的导函数,由函数在x=0时的导数等于2,求得a的值;
(2)构造函数g(x)=f(x)-2x-$\frac{2{x}^{3}}{3}$,求其导函数,判断导函数在[0,1)上的符号,得到原函数在[0,1)上的单调性,由此可得使不等式恒成立的实数M的取值范围.
解答 解:(1)由f(x)=ln(a+x)-ln(a-x)(a>0),
得f′(x)=$\frac{1}{a+x}$+$\frac{1}{a-x}$,
∴在点(0,f(0))处的切线斜率为f′(0)=$\frac{2}{a}$,
∵曲线y=f(x)在点(0,f(0))处的切线方程为y=2x,
∴f′(0)=2,
即$\frac{2}{a}$=2,解得a=1;
(2)令g(x)=f(x)-2x-$\frac{2{x}^{3}}{3}$=ln(1+x)-ln(1-x)
则g′(x)=$\frac{1}{1+x}$+$\frac{1}{1-x}$-2-2x2=$\frac{2{x}^{4}}{1-{x}^{2}}$≥0在[0,1)恒成立,
即有函数g(x)在[0,1)上为增函数,
则g(x)≥g(0)=0,即g(x)的最小值为0,
由题意可得M≤g(x)的最小值,可得M的范围是(-∞,0].
点评 本题考查导数的运用:求切线的斜率和单调性,考查不等式恒成立问题的解法,注意运用参数分离和函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
1.设f(x)=($\frac{1}{m}$)|x|,m>1,x∈R,那么f(x)是( )
| A. | 偶函数且在(0,+∞)上是增函数 | B. | 奇函数且在(0,+∞)上是增函数 | ||
| C. | 偶函数且在(0,+∞)上是减函数 | D. | 奇函数且在(0,+∞)上是减函数 |
19.函数$f(x)=\frac{lg(x+2)}{x+1}$的定义域是( )
| A. | (-∞,-1)∪(-1,+∞) | B. | (-2,+∞) | C. | (-2,-1)∪(-1,+∞) | D. | [-2,-1)∪(-1,+∞) |
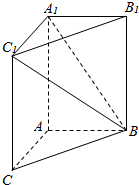 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.