题目内容

．
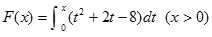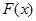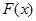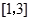（1）求的单调区间；（2）求函数在上的最值.
（1）单调增区间是，单调递减区间是;（2）最大值是，最小值是．

试题分析：（1）首先利用牛顿-莱布尼兹公式求出函数的表达式，并注意题中所给的定义域为，再利用导数通过解不等式及并与定义域取交集而求得函数的单调区间；（2）求函数最值的一般步骤:①求出函数在给定区间上的极值及区间的端点所对应的函数值;②比较上述值的大小;③得结论:其中最大者即为函数的最大值,最小者即为函数的最小值.
试题解析：依题意得，，定义域是．
（1）,
令，得或，
令，得
由于定义域是，
函数的单调增区间是，单调递减区间是．
（2）令，得，
由于，，，
在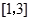上的最大值是，最小值是．
练习册系列答案
相关题目
已知函数f（x）=alnx-ax-3（a∈R），
（1）若函数y=f（x）在点（2，f（2））处的切线斜率为1，求a的值；
（2）在（1）的条件下，对任意t∈[1，2]，函数g（x）=x3+x2[
m
2
+f′（x）]在区间（t，3）总存在极值，求m的取值范围；
（3）若a=2，对于函数h（x）=（p-2）x-
p+2e
x
-3在[1，e]上至少存在一个x0使得h（x0）＞f（x0）成立，求实数P的取值范围．
已知函数f（x）=a（lnx-x）（a∈R）．
（I）讨论函数f（x）的单调性；
（II）若函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，函数g（x）=x3+x2[
m
2
+f′(x)]在区间（2，3）上总存在极值，求实数m的取值范围．
A、B两地相距1千米，B、C两地相距3千米，甲从A地出发，经过B前往C地，乙同时从B地出发，前往C地．甲、乙的速度关于时间的关系式分别为和（单位：千米/小时）．甲、乙从起点到终点的过程中，给出下列描述：
①出发后1小时，甲还没追上乙             ② 出发后1小时，甲乙相距最远
③甲追上乙后，又被乙追上，乙先到达C地   ④甲追上乙后，先到达C地 
其中正确的是         ．（请填上所有描述正确的序号）
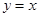直线与抛物线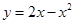，所围成封闭图形的面积为   
计算定积分：=_______.
若则（   ）
A．B．C．D．1
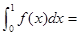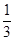
设函数的图象与直线轴所围成的图形的面积称为在上的面积，则函数上的面积为          ．
定积分等于（   ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网