题目内容
已知函数f(x)=
.
(1)求f(x)的最大值;
(2)若对所有x≥1都有f(x)≥
,求实数k的取值范围.
| 1+1nx |
| x |
(1)求f(x)的最大值;
(2)若对所有x≥1都有f(x)≥
| k |
| x+1 |
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:(1)易求f′(x)=-
,易证当x∈(0,1)时,f′(x)>0,f(x)递增,当x∈(1,+∞)时,f′(x)<0,f(x)递减;从而可求f(x)的最大值;
(2)依题意,)对于任意的x≥1,f(x)≥
?k≤
(x≥1),构造函数g(x)=
(x≥1),利用导数法可判断出g(x)在[1,+∞)上递增,从而可求g(x)min,继而可得k的取值范围.
| lnx |
| x2 |
(2)依题意,)对于任意的x≥1,f(x)≥
| k |
| x+1 |
| (x+1)(1+lnx) |
| x |
| (x+1)(1+lnx) |
| x |
解答:
解:(1)f′(x)=
=-
,
当x∈(0,1)时,f′(x)>0,f(x)递增;
当x∈(1,+∞)时,f′(x)<0,f(x)递减;
∴f(x)max=f(1)=1;
(2)对于任意的x≥1,f(x)≥
,即k≤
(x≥1),
设g(x)=
(x≥1),则k≤g(x)min;
∵g(x)=1+
+lnx+
,
∴g′(x)=
,
令h(x)=x-lnx(x≥1),则h′(x)=1-
=
≥0(仅当x=1时取等号),
∴h(x)在[1,+∞)上递增,
∴h(x)≥h(1)=1>0,
∴g′(x))=
>0,
∴g(x)在[1,+∞)上递增,
∴g(x)≥g(1)=2,即g(x)min=2,
∴k≤2,即实数k的取值范围为(-∞,2].
| ||
| x2 |
| lnx |
| x2 |
当x∈(0,1)时,f′(x)>0,f(x)递增;
当x∈(1,+∞)时,f′(x)<0,f(x)递减;
∴f(x)max=f(1)=1;
(2)对于任意的x≥1,f(x)≥
| k |
| x+1 |
| (x+1)(1+lnx) |
| x |
设g(x)=
| (x+1)(1+lnx) |
| x |
∵g(x)=1+
| 1 |
| x |
| lnx |
| x |
∴g′(x)=
| x-lnx |
| x2 |
令h(x)=x-lnx(x≥1),则h′(x)=1-
| 1 |
| x |
| x-1 |
| x |
∴h(x)在[1,+∞)上递增,
∴h(x)≥h(1)=1>0,
∴g′(x))=
| x-lnx |
| x2 |
∴g(x)在[1,+∞)上递增,
∴g(x)≥g(1)=2,即g(x)min=2,
∴k≤2,即实数k的取值范围为(-∞,2].
点评:本题考查函数恒成立问题,着重考查函数的单调性与极值,考查构造函数思想与导数法的综合运用,属于难题.

练习册系列答案
相关题目
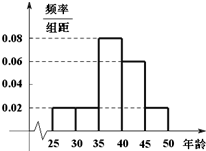 某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.