题目内容
若a1x≤sinx≤a2x对任意的 都成立,则a2-a1的最小值为________.
都成立,则a2-a1的最小值为________.
1-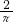
分析:确定 时,y=sinx在直线y=x下方,在直线y=
时,y=sinx在直线y=x下方,在直线y=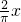 上方,由此可求a2-a1的最小值.
上方,由此可求a2-a1的最小值.
解答:y=sinx求导可得y′=cosx,则x=0时,y′=1,∴ 时,y=sinx的图象与直线y=x相切,
时,y=sinx的图象与直线y=x相切,
过点( ,1),(0,0)的直线方程为y=
,1),(0,0)的直线方程为y=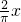
则 时,y=sinx在直线y=x下方,在直线y=
时,y=sinx在直线y=x下方,在直线y=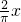 上方
上方
∴a1x≤sinx≤a2x对任意的 都成立时,a2-a1的最小值为1-
都成立时,a2-a1的最小值为1-
故答案为:1-
点评:本题考查直线的两个特殊位置,考查恒成立问题,属于中档题.
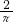
分析:确定
 时,y=sinx在直线y=x下方,在直线y=
时,y=sinx在直线y=x下方,在直线y=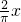 上方,由此可求a2-a1的最小值.
上方,由此可求a2-a1的最小值.解答:y=sinx求导可得y′=cosx,则x=0时,y′=1,∴
 时,y=sinx的图象与直线y=x相切,
时,y=sinx的图象与直线y=x相切,过点(
 ,1),(0,0)的直线方程为y=
,1),(0,0)的直线方程为y=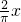
则
 时,y=sinx在直线y=x下方,在直线y=
时,y=sinx在直线y=x下方,在直线y=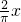 上方
上方∴a1x≤sinx≤a2x对任意的
 都成立时,a2-a1的最小值为1-
都成立时,a2-a1的最小值为1-
故答案为:1-

点评:本题考查直线的两个特殊位置,考查恒成立问题,属于中档题.

练习册系列答案
相关题目
 都成立,则a2-a1的最小值为 .
都成立,则a2-a1的最小值为 . 都成立,则a2-a1的最小值为 .
都成立,则a2-a1的最小值为 .