题目内容
已知函数y=lg(-x2+x+2)的定义域为A,指数函数y=ax(a>0且a≠1)(x∈A)的值域为B.(1)若a=2,求A∪B;
(2)若A∩B=(
 ,2),求a的值.
,2),求a的值.
【答案】分析:(1)先根据真数大于零求出集合A以及指数函数的值域集合B,再根据两个集合的交集的意义求解;
(2)先根据真数大于零求出集合A,讨论a>1与0<a<1两种情形,由A∩B=( ,2)建立关系式,解之即可.
,2)建立关系式,解之即可.
解答:解:(1)依题意知A={x|-x2+x-2>0}=(-1,2).(2分)
若a=2,则y=ax=2x∈( ,4),即B=(
,4),即B=( ,4),(4分)
,4),(4分)
∴A∪B=(-1,4).( )(6分)
(2)由A={x|-x2+x-2>0}=(-1,2),知
①当a>1时,B=(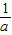 ,a2),若A∩B=(
,a2),若A∩B=( ,2),则必有
,2),则必有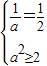 ,a=2(10分)
,a=2(10分)
(或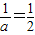 ,a=2此时B=(
,a=2此时B=( ,2),A∩B=(
,2),A∩B=( ,2),符合题意,故a=2为所求).
,2),符合题意,故a=2为所求).
②当0<a<1时,B=(a2,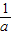 ),若A∩B=(
),若A∩B=( ,2),则必有
,2),则必有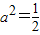 ,
,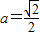 ,此时B=(
,此时B=( ,
,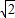 ),A∩B=(
),A∩B=( ,
,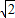 ),不符合题意,舍去;(13分)
),不符合题意,舍去;(13分)
综上可知a=2.(14分)
点评:本题主要考查了指数函数与对数函数的定义域和值域,以及交集与并集的运算,属于基础题.
(2)先根据真数大于零求出集合A,讨论a>1与0<a<1两种情形,由A∩B=(
 ,2)建立关系式,解之即可.
,2)建立关系式,解之即可.解答:解:(1)依题意知A={x|-x2+x-2>0}=(-1,2).(2分)
若a=2,则y=ax=2x∈(
 ,4),即B=(
,4),即B=( ,4),(4分)
,4),(4分)∴A∪B=(-1,4).( )(6分)
(2)由A={x|-x2+x-2>0}=(-1,2),知
①当a>1时,B=(
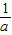 ,a2),若A∩B=(
,a2),若A∩B=( ,2),则必有
,2),则必有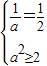 ,a=2(10分)
,a=2(10分)(或
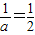 ,a=2此时B=(
,a=2此时B=( ,2),A∩B=(
,2),A∩B=( ,2),符合题意,故a=2为所求).
,2),符合题意,故a=2为所求).②当0<a<1时,B=(a2,
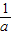 ),若A∩B=(
),若A∩B=( ,2),则必有
,2),则必有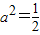 ,
,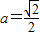 ,此时B=(
,此时B=( ,
,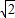 ),A∩B=(
),A∩B=( ,
,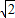 ),不符合题意,舍去;(13分)
),不符合题意,舍去;(13分)综上可知a=2.(14分)
点评:本题主要考查了指数函数与对数函数的定义域和值域,以及交集与并集的运算,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目