题目内容
已知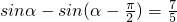 ,且
,且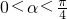 .
.
(Ⅰ)求sinαcosα、sinα-cosα的值;
(Ⅱ)求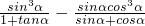 的值.
的值.
解:(Ⅰ) 由已知 sinα+cosα= …①,
…①,
①式平方得:1+2sinαcosα= …(2分)
…(2分)
∴sinαcosα= …②…(4分)
…②…(4分)
(sinα-cosα)2=sin2α-2sinα•cosα+cos2α
将②代入得:
(sinα-cosα)2=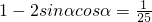
又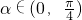
∴sinα<cosα
∴sinα-cosα=- …(6分)
…(6分)
(Ⅱ)
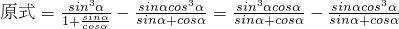
=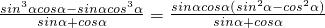
= …(12分)
…(12分)
分析:(Ⅰ)利用诱导公式转化已知条件,通过平方同角三角函数的基本关系式,求sinαcosα,然后对sinα-cosα平方代入sinαcosα的值,利用角的范围即可求出sinα-cosα的值;
(Ⅱ)利用切化弦,同分把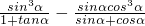 化简为(Ⅰ)所求出的值,代入求解即可.
化简为(Ⅰ)所求出的值,代入求解即可.
点评:本题是中档题,考查三角函数的基本公式的应用,解题的关键是角的范围与三角函数的值的大小的比较,切化弦的应用.
 …①,
…①,①式平方得:1+2sinαcosα=
 …(2分)
…(2分)∴sinαcosα=
 …②…(4分)
…②…(4分)(sinα-cosα)2=sin2α-2sinα•cosα+cos2α
将②代入得:
(sinα-cosα)2=
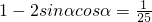
又
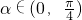
∴sinα<cosα
∴sinα-cosα=-
 …(6分)
…(6分)(Ⅱ)
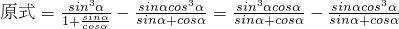
=
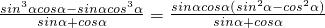
=
 …(12分)
…(12分)分析:(Ⅰ)利用诱导公式转化已知条件,通过平方同角三角函数的基本关系式,求sinαcosα,然后对sinα-cosα平方代入sinαcosα的值,利用角的范围即可求出sinα-cosα的值;
(Ⅱ)利用切化弦,同分把
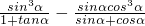 化简为(Ⅰ)所求出的值,代入求解即可.
化简为(Ⅰ)所求出的值,代入求解即可.点评:本题是中档题,考查三角函数的基本公式的应用,解题的关键是角的范围与三角函数的值的大小的比较,切化弦的应用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,当点P在⊙F1上运动时M形成曲线C.(如图)
,当点P在⊙F1上运动时M形成曲线C.(如图)