Question

【题目】已知下列命题：

①函数在上单调递减，在上单调递增；

②若函数在上有两个零点，则的取值范围是；

③函数在上单调递减；

④当时，函数的最大值为.

上述命题正确的是__________（填序号）.

Answer 1

【答案】①②③

【解析】

根据复合函数单调性可判断出①正确；利用数形结合的方式可确定当与有两个交点时的范围，知②正确；利用整体对应法判断正弦型函数的单调性，可确定③正确；利用基本不等式可求得函数最大值，知④错误.

①在上单调递减，在上单调递增；在上单调递增，在上单调递减，在上单调递增，①正确；

②令，则在上有两个零点等价于与有两个交点；

在平面直角坐标系中作出与的图象如下图所示：

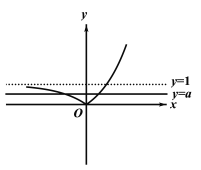
由图象可知：若与有两个交点，则，②正确；

③，

当时，，此时单调递减，③正确；

④当时，，

（当且仅当，即时取等号），

，④错误.

故答案为：①②③.