题目内容
9.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点F恰好与抛物线y2=8x的焦点F重合,且两曲线的一个交点为P,若|PF|=5,则双曲线的方程为( )| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{32}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
分析 求出抛物线的焦点坐标,顶点双曲线方程$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)焦距,得到ab关系,求出P的坐标,把P点代入双曲线方程求出双曲线的标准方程.
解答 解:∵抛物线y2=8x的焦点F(2,0),
∴由题意知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F(2,0),
∴a2+b2=4,
∵P是抛物线与双曲线的一个交点,|PF|=5,
∴p点横坐标xP=3,代入抛物线y2=8x得P(3,±2$\sqrt{6}$),
把P(3,±2$\sqrt{6}$)代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)得$\frac{9}{{a}^{2}}-\frac{24}{{b}^{2}}=1$,整理,得a4-37a2+36=0,
解得a2=1,或a2=36(舍)
则b2=3,
所求双曲线方程为:x2-$\frac{{y}^{2}}{3}$=1.
故选:D.
点评 本题考查双曲线的方程的求法,抛物线的简单性质的应用,是中档题,解题时要熟练掌握抛物线、双曲线的简单性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.设过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,c=$\sqrt{{a}^{2}-{b}^{2}}$)的左焦点与上顶点的直线为l,若坐标原点O到直线l的距离为$\frac{c}{2}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
17.不等式组$\left\{\begin{array}{l}2x+y-5≤0\\ 3x-y≥0\\ x-2y≤0\end{array}\right.$的解集记为D,$z=\frac{y+1}{x+1}$,有下面四个命题:
p1:?(x,y)∈D,z≥1;p2:?(x,y)∈D,z≥1
p3:?(x,y)∈D,z≤2;p4:?(x,y)∈D,z<0
其中的真命题是( )
p1:?(x,y)∈D,z≥1;p2:?(x,y)∈D,z≥1
p3:?(x,y)∈D,z≤2;p4:?(x,y)∈D,z<0
其中的真命题是( )
| A. | p1,p2 | B. | p1,p3 | C. | p1,p4 | D. | p2,p3 |
4.已知全集U={l,2,3,4,5},集合A={2,3,4},B={l,4}则(∁UA)∩B为( )
| A. | {1} | B. | {1,5} | C. | {1,4} | D. | {1,4,5} |
14.已知等比数列{an}的各项均为正数,$\overrightarrow{a}$=(2,a3),$\overrightarrow{b}$=(-8,a13),a⊥b,若am=4,则m为( )
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
18.已知线性回归直线方程是$\stackrel{∧}{y}$=1.23x+0.08,求m的值.
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | m | 6.5 | 7.0 |
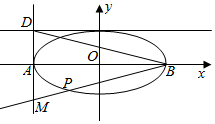 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.