题目内容
由直线y=0与曲线y=sinx在x∈[0，2π]内所围成的封闭图形的面积为________．
4
分析：根据对称性，确定被积函数与被积区间，用定积分表示面积，即可求得结论．
解答：由题意，根据对称性可得直线y=0与曲线y=sinx在x∈[0，2π]内所围成的封闭图形的面积为
=2（-cosx）
=-2cosπ+2cos0=4
故答案为：4
点评：本题考查利用定积分求面积，解题的关键是确定被积函数与被积区间，属于基础题．
分析：根据对称性，确定被积函数与被积区间，用定积分表示面积，即可求得结论．
解答：由题意，根据对称性可得直线y=0与曲线y=sinx在x∈[0，2π]内所围成的封闭图形的面积为
=2（-cosx）=-2cosπ+2cos0=4故答案为：4
点评：本题考查利用定积分求面积，解题的关键是确定被积函数与被积区间，属于基础题．
练习册系列答案
相关题目
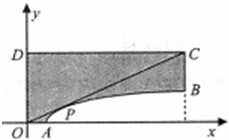已知图形OAPBCD是由不等式组