题目内容
若tanα=4, ,则tan(α+β)=
,则tan(α+β)=
- A.-

- B.

- C.-
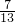
- D.

A
分析:利用同角三角函数的关系求出tanβ=3,,利用两角和的正切公式求出tan(α+β)的值.
解答:因为 ,
,
所以tanβ=3,
所以tan(α+β)= =
=
故选A.
点评:利用同角三角函数的基本关系式解决问题:(1)已知某角的一个三角函数值,求该角的其它三角函数值的方法.(2)求值时要注意各三角函数的符号,必要时分类讨论.(3)三角函数式的化简的方法和结果应满足要求.
分析:利用同角三角函数的关系求出tanβ=3,,利用两角和的正切公式求出tan(α+β)的值.
解答:因为
 ,
,所以tanβ=3,
所以tan(α+β)=
 =
=
故选A.
点评:利用同角三角函数的基本关系式解决问题:(1)已知某角的一个三角函数值,求该角的其它三角函数值的方法.(2)求值时要注意各三角函数的符号,必要时分类讨论.(3)三角函数式的化简的方法和结果应满足要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目