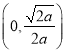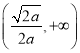题目内容
【题目】已知![]() ,函数
,函数![]() ,
, ![]() .(
.(![]() 的图象连续不断)
的图象连续不断)
(1) 求![]() 的单调区间;
的单调区间;
(2) 当![]() 时,证明:存在
时,证明:存在![]() ,使
,使![]() ;
;
(3) 若存在属于区间![]() 的
的![]() ,且
,且![]() ,使
,使![]() ,证明:
,证明: ![]() .
.
【答案】(Ⅰ)解: ![]() , 令
, 令
![]()
![]() .
.
当x变化时, ![]() 的变化情况如下表:
的变化情况如下表:
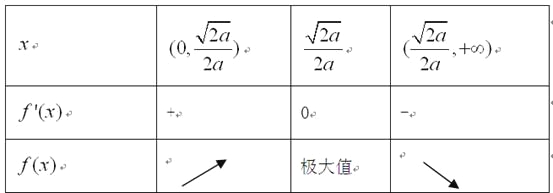
所以, ![]() 的单调递增区间是
的单调递增区间是![]() 的单调递减区间是
的单调递减区间是![]()
(Ⅱ)证明:当![]()
由(Ⅰ)知![]() 在(0,2)内单调递增,在
在(0,2)内单调递增,在![]() 内单调递减.令
内单调递减.令![]()
由于![]() 在(0,2)内单调递增,故
在(0,2)内单调递增,故![]() 取
取![]()
所以存在![]() 即存在
即存在![]()
(Ⅲ)证明:由![]() 及(Ⅰ)的结论知
及(Ⅰ)的结论知![]() ,
,
从而![]() 上的最小值为
上的最小值为![]() 又由
又由![]() ,
,![]() 知
知![]()
故![]()
从而![]()
【解析】试题分析:(1)求![]() 的单调区间,由于函数
的单调区间,由于函数![]() 含有对数函数,因此求
含有对数函数,因此求![]() 的单调区间,可用导数法,因此对函数
的单调区间,可用导数法,因此对函数![]() 求导得,
求导得, ![]() ,令
,令![]() ,解得
,解得![]() ,列表确定单调区间;(2)当
,列表确定单调区间;(2)当![]() 时,证明:存在
时,证明:存在![]() ,使
,使![]() ,可转化为
,可转化为![]() 在
在![]() 上有解,可令
上有解,可令![]() ,有根的存在性定理可知,只要在
,有根的存在性定理可知,只要在![]() 找到两个
找到两个![]() ,是得
,是得![]() 即可,故本题把
即可,故本题把![]() 代入
代入![]() 得
得![]() ,由(1)知
,由(1)知![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减, ![]() ,故
,故![]() ,取
,取![]() ,则
,则![]() ,即可证出;(3)若存在均属于区间
,即可证出;(3)若存在均属于区间![]() 的
的![]() ,且
,且![]() ,使
,使![]() ,由(1)知
,由(1)知![]() 的单调递增区间是
的单调递增区间是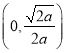 ,单调递减区间是
,单调递减区间是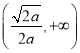 ,故
,故![]() ,且
,且![]() 在
在![]() 上的最小值为
上的最小值为![]() ,而
,而![]() ,
, ![]() ,只有
,只有![]() ,由单调性可知,
,由单调性可知, 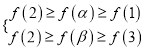 ,从而可证得结论.
,从而可证得结论.
试题解析:(1)![]() (1分)
(1分)
令![]() ,解得
,解得![]() (2分)
(2分)
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
| |
| + | 0 | - | |
| 递增 | 极大值 | 递减 |
所以, ![]() 的单调递增区间是
的单调递增区间是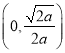 ,单调递减区间是
,单调递减区间是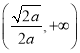 (5分)
(5分)
(2)证明:当![]() 时,
时, ![]() ,
,
由(1)知![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减.
内单调递减.
令![]() . (6分)
. (6分)
由于![]() 在
在![]() 内单调递增,故
内单调递增,故![]() ,即
,即![]() (7分)
(7分)
取![]() ,则
,则![]() .
.
所以存在![]() ,使
,使![]() ,
,
即存在![]() ,使
,使![]() . (
. (
(说明: ![]() 的取法不唯一,只要满足
的取法不唯一,只要满足![]() ,且
,且![]() 即可.)
即可.)
(3)证明:由![]() 及(1)的结论知
及(1)的结论知![]() ,
,
从而![]() 在
在![]() 上的最小值为
上的最小值为![]() , (10分)
, (10分)
又由![]() ,
, ![]() ,知
,知![]() (11分)
(11分)
故 即
即![]() (13分)
(13分)
从而![]() (14分)
(14分)

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目