题目内容
等差数列{an}中a3=7,a1+a2+a3=12,记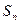 为{an}的前n项和,令bn=anan+1,数列
为{an}的前n项和,令bn=anan+1,数列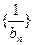 的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<
的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<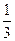 ;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.
;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.
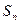 为{an}的前n项和,令bn=anan+1,数列
为{an}的前n项和,令bn=anan+1,数列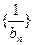 的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<
的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<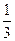 ;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.
;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.(Ⅰ) Sn= (Ⅱ) 略 (Ⅲ)m=2,n=16
(Ⅱ) 略 (Ⅲ)m=2,n=16
 (Ⅱ) 略 (Ⅲ)m=2,n=16
(Ⅱ) 略 (Ⅲ)m=2,n=16解(1)设数列 的公差为
的公差为 ,由
,由
 ,
, .
.
解得 ,
, ="3 " …2分∴
="3 " …2分∴ ; ……3分 Sn=
; ……3分 Sn= 4分
4分
(2)
∴ ……………………… 6分
……………………… 6分
∴ =
= … 8分
… 8分 …… 9分
…… 9分
(3)由(2)知, ∴
∴ ,
,
∵ 成等比数列.∴
成等比数列.∴ 即
即 …… 11分
…… 11分
当m=1时,7 ,
, =1,不合题意;
=1,不合题意;
当m=2时,
 ,
, =16,符合题意;
=16,符合题意;
当m=3时,
 ,
, 无正整数解;
无正整数解;
当m=4时,
 ,
, 无正整数解;
无正整数解;
当m=5时,
 ,
, 无正整数解;
无正整数解;
当m=6时,
 ,
, 无正整数解;…… 14分(少讨论一个扣0.5分)
无正整数解;…… 14分(少讨论一个扣0.5分)
当m≥7时, ,
,
则 ,而
,而 ,
,
所以,此时不存在正整数m,n,且7<m<n,使得 成等比数列.……15分
成等比数列.……15分
综上,存在正整数m=2,n=16,且1<m<n,使得 成等比数列.… 16分
成等比数列.… 16分
 的公差为
的公差为 ,由
,由 ,
, .
.解得
 ,
, ="3 " …2分∴
="3 " …2分∴ ; ……3分 Sn=
; ……3分 Sn= 4分
4分(2)

∴
 ……………………… 6分
……………………… 6分∴
 =
= … 8分
… 8分 …… 9分
…… 9分(3)由(2)知,
 ∴
∴ ,
,
∵
 成等比数列.∴
成等比数列.∴ 即
即 …… 11分
…… 11分当m=1时,7
 ,
, =1,不合题意;
=1,不合题意;当m=2时,

 ,
, =16,符合题意;
=16,符合题意;当m=3时,

 ,
, 无正整数解;
无正整数解;当m=4时,

 ,
, 无正整数解;
无正整数解;当m=5时,

 ,
, 无正整数解;
无正整数解;当m=6时,

 ,
, 无正整数解;…… 14分(少讨论一个扣0.5分)
无正整数解;…… 14分(少讨论一个扣0.5分)当m≥7时,
 ,
,则
 ,而
,而 ,
,所以,此时不存在正整数m,n,且7<m<n,使得
 成等比数列.……15分
成等比数列.……15分综上,存在正整数m=2,n=16,且1<m<n,使得
 成等比数列.… 16分
成等比数列.… 16分
练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
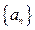 前n项和记为
前n项和记为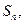
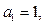
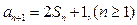 ,
,
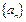 的的通项公式;(Ⅱ)等差数列
的的通项公式;(Ⅱ)等差数列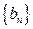 的各项为正,其前n项和为
的各项为正,其前n项和为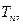 且
且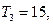 又
又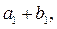
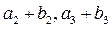 成等比数列,求
成等比数列,求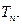
 是正项数列
是正项数列 的前n项和且
的前n项和且
 (2)
(2)
 (n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是
(n∈N+)是数列{an}的倒均数. (1)若数列{an}的倒均数是 ,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q =
,求数列{an}的通项公式;(2)若等比数列{bn}的首项为–1,公比为q = ,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.
,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.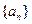 的前
的前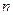 项和为
项和为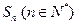 ,关于数列
,关于数列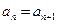 ;
;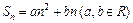 ,则数列
,则数列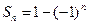 ,则数列
,则数列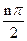 )an+sin
)an+sin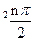 ,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=
,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=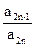 ,令 Sn=
,令 Sn=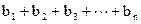 求Sn
求Sn 为偶函数且
为偶函数且 ,当
,当 时,
时, ,若
,若 ,
, 。
。