题目内容
以椭圆等 的顶点为顶点,离心率为2的双曲线的方程为
的顶点为顶点,离心率为2的双曲线的方程为
- A.
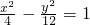
- B.

- C.
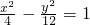 或
或
- D.
C
分析:先确定椭圆的顶点坐标,再分类讨论,利用离心率为2,即可求得双曲线的方程.
解答:椭圆 的顶点坐标为(±2,0),(0,±1)
的顶点坐标为(±2,0),(0,±1)
若双曲线的顶点坐标为(±2,0),则a=2,∵离心率为2,∴c=4,∴b2=c2-a2=12,
∴双曲线的方程为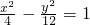 ;
;
若双曲线的顶点坐标为(0,±1),则a=1,∵离心率为2,∴c=2,∴b2=c2-a2=3,
∴双曲线的方程为
综上,双曲线的方程为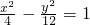 或
或
故选C.
点评:本题考查双曲线的标准分析,考查椭圆的几何性质,属于中档题.
分析:先确定椭圆的顶点坐标,再分类讨论,利用离心率为2,即可求得双曲线的方程.
解答:椭圆
 的顶点坐标为(±2,0),(0,±1)
的顶点坐标为(±2,0),(0,±1)若双曲线的顶点坐标为(±2,0),则a=2,∵离心率为2,∴c=4,∴b2=c2-a2=12,
∴双曲线的方程为
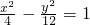 ;
;若双曲线的顶点坐标为(0,±1),则a=1,∵离心率为2,∴c=2,∴b2=c2-a2=3,
∴双曲线的方程为

综上,双曲线的方程为
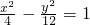 或
或
故选C.
点评:本题考查双曲线的标准分析,考查椭圆的几何性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•广东模拟)已知椭圆C1:
(2013•广东模拟)已知椭圆C1: 的顶点为顶点,离心率为2的双曲线的方程为( )
的顶点为顶点,离心率为2的双曲线的方程为( )

 或
或
