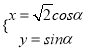题目内容
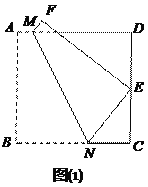
【题目】如图甲,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 与
与![]() 的交点,将
的交点,将![]() 沿
沿![]() 折起到
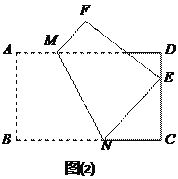
折起到![]() 的位置,如图乙.
的位置,如图乙.
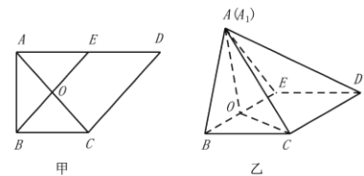
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)由已知可得![]() ,所以欲证
,所以欲证![]() 平面
平面![]() ,只要证
,只要证![]() 平面
平面![]() 即可,即证
即可,即证![]() 且
且![]() 即可,由
即可,由![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,可得
,可得![]() ,即
,即![]() ,
,![]() ,可证结论成立;(Ⅱ)等体积法求距离,即设点
,可证结论成立;(Ⅱ)等体积法求距离,即设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() ,求之即可.
,求之即可.
试题解析: (Ⅰ)证明:在图甲中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,
![]() ,…………(2分)
,…………(2分)
即在图乙中,![]() ,
,![]() .………(3分)
.………(3分)

又![]() ,
,![]() 平面
平面![]() .……(4分)
.……(4分)
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,…………(5分)
,…………(5分)
![]() 平面
平面![]() .…(6分)
.…(6分)
(Ⅱ)解:由已知,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,………(7分)
,………(7分)
![]() ,又由(Ⅰ)知,
,又由(Ⅰ)知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() .
.
![]() ,
,![]() .……(9分)
.……(9分)
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
由![]() 得:
得:![]() ,(11分)
,(11分)
![]() ,故
,故![]() 到平面
到平面![]() 的距离为
的距离为![]() .…(12分)
.…(12分)

练习册系列答案
相关题目