题目内容
已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
分析:极坐标系下的问题,我们都将其转化为直角坐标系下来加以解决,利用点到直线的距离公式求解即可.
解答:解:曲线ρ=2sinθ化为普通方程x2+y2=2y,直线ρsin(θ+
)=4化为普通方程为
x+y-8=0
圆的圆心为(0,1),半径R为1,圆心到直线的距离d=
=
所以圆上点到直线距离的最小值为
-1=
| π |
| 3 |
| 3 |
圆的圆心为(0,1),半径R为1,圆心到直线的距离d=
| |1-8| | ||
|
| 7 |
| 2 |
所以圆上点到直线距离的最小值为
| 7 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查了圆上点到某条直线的距离的最大值、最小值为圆心到直线的距离加半径、减半径,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
(1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线 选做题:(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题:(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 的距离的最小值是 .
的距离的最小值是 . 的最小值是 .
的最小值是 .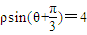 的距离的最小值是 .
的距离的最小值是 .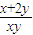 的最小值是 .
的最小值是 .