题目内容
11．函数f（x）=$\frac{x-2}{x-1}$的图象关于（ ）| A． | y轴对称 | B． | 直线y=-x对称 | C． | 坐标原点对称 | D． | 直线y=x对称 |
分析 根据函数图象的平移即可得到答案．
解答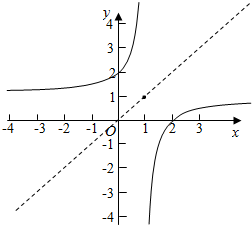 
解：f（x）=$\frac{x-2}{x-1}$=$\frac{x-1-1}{x-1}$=1-$\frac{1}{x-1}$，如图所示：
∵y=-$\frac{1}{x}$关于原点对称，和关于y=x对称，
∴f（x）关于（1，1）对称，和关于y=x对称，
故选：D．
点评 本题考查了函数图象的识别，属于基础题．
练习册系列答案
相关题目
19．定义在R上的函数f（x）在（8，+∞）满足对任意x1，x2∈（8，+∞），并且x1≠x2有$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜0成立，并且函数y=f（x+8）为偶函数，则有（ ）
| A． | f（6）＞f（7） | B． | f（6）＞f（9） | C． | f（7）＞f（9） | D． | f（7）＞f（10） |