Question

（本小题满分12分）已知，函数，．

（1）若曲线与曲线在它们的交点处的切线重合，求，的值；

（2）设，若对任意的，且，都有，求的取值范围．

Answer 1

（1）；（2）．

【解析】

试题分析：（1）由已知得 ， ，从而由且即可求得，的值；

（2）由 可得，；令，只需求使在单调递增的的取值范围即可，即求使在恒成立的的取值范围即可，利用分离参数法转化为一个函数的最小值问题，即可求得的的取值范围．

试题解析： （1），.，

由题意，，，.

又因为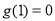，.,得 4分

（2）由 可得，

令，只需证在单调递增即可 8分

只需说明在恒成立即可 10分

即，

故， 12分

（如果考生将视为斜率，利用数形结合得到正确结果的，则总得分不超过8分）

考点：1．导数的几何意义；2．利用导数研究函数的单调性．