题目内容
已知椭圆C: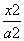 +
+ =1(a>b>0)的右焦点为F(1,0),右顶点为A,且|AF|=1.
=1(a>b>0)的右焦点为F(1,0),右顶点为A,且|AF|=1.
(1)求椭圆C的标准方程;
(2)若动直线l:y=kx+m与椭圆C有且只有一个交点P,且与直线x=4交于点Q,问:是否存在一个定点M(t,0),使得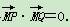 .若存在,求出点M的坐标;若不存在,说明理由.
.若存在,求出点M的坐标;若不存在,说明理由.
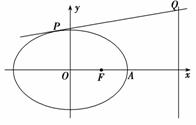
【解】 (1)由c=1,a-c=1,得a=2,∴b= ,
,
故椭圆C的标准方程为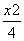 +
+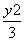 =1.
=1.
(2)由 得:(3+4k2)x2+8kmx+4m2-12=0,
得:(3+4k2)x2+8kmx+4m2-12=0,
∴Δ=64k2m2-4(3+4k2)(4m2-12)=0,即m2=3+4k2.
设P(xp,yp),
∵M(t,0),Q(4,4k+m),
 恒成立,故
恒成立,故 ,
,
即t=1.
∴存在点M(1,0)符合题意.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
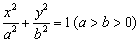 的离心率
的离心率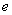 为黄金分割比
为黄金分割比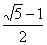 ,则称该椭圆为“优美椭圆”,该类椭圆具有性质
,则称该椭圆为“优美椭圆”,该类椭圆具有性质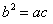 (
(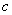 为该椭圆的半焦距).那么在双曲线
为该椭圆的半焦距).那么在双曲线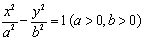 中具有类似性质的“优美双曲线”的离心率为 ( )
中具有类似性质的“优美双曲线”的离心率为 ( )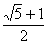 C.
C.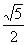 D.
D.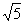
 上产生两个随机数n和m,则方程
上产生两个随机数n和m,则方程 有实根的概率为________.
有实根的概率为________.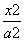 +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:(x-3)2+(y-1)2=3相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:(x-3)2+(y-1)2=3相切.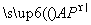 ·
·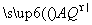 =0,求证:直线l过定点,并求该定点的坐标.
=0,求证:直线l过定点,并求该定点的坐标.
 函数
函数 定义如下:当
定义如下:当 时,
时, 当
当 时,
时, 那么
那么 无最小值
无最小值 的前n项和为
的前n项和为 且
且
 , 记
, 记 证明:
证明:
 B.
B. C.
C. D.以上答案均不对
D.以上答案均不对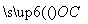 =m
=m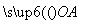 +n
+n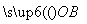 ,则m+n的取值范围是( )
,则m+n的取值范围是( )