题目内容
已知圆 ,直线
,直线
 ,
,
(1)求证:直线 与圆
与圆 恒相交;
恒相交;
(2)当 时,过圆
时,过圆 上点
上点 作圆的切线
作圆的切线 交直线
交直线 于
于 点,
点, 为圆
为圆 上的动点,求
上的动点,求 的取值范围;
的取值范围;
 ,直线
,直线
 ,
,(1)求证:直线
 与圆
与圆 恒相交;
恒相交;(2)当
 时,过圆
时,过圆 上点
上点 作圆的切线
作圆的切线 交直线
交直线 于
于 点,
点, 为圆
为圆 上的动点,求
上的动点,求 的取值范围;
的取值范围;(1) 恒过两直线
恒过两直线 及
及 的交点
的交点 ;(2)
;(2) 。
。
 恒过两直线
恒过两直线 及
及 的交点
的交点 ;(2)
;(2) 。
。试题分析:(1)证明:由
 得方程得
得方程得 ,
,故
 恒过两直线
恒过两直线 及
及 的交点
的交点 ,
, ,即点
,即点 在圆
在圆 内部,
内部, 直线
直线 与圆
与圆 恒相交。
恒相交。(2)由题知

 时,
时,
所以


 ,而
,而 ,所以
,所以
点评:定点直线系:若
 :
: =0和
=0和 :
: =0相交,则过
=0相交,则过 与
与 交点的直线系为
交点的直线系为 +λ
+λ =0。
=0。
练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
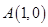 和点
和点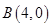 到直线
到直线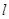 的距离依次为
的距离依次为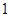 和
和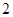 ,则这样的直线有( )
,则这样的直线有( )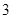 条
条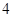 条
条 上,则圆C的标准方程为 。
上,则圆C的标准方程为 。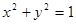 和
和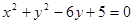 的位置关系为( )
的位置关系为( ) 和
和 的位置关系为( )
的位置关系为( )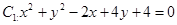 和圆
和圆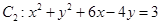 的位置关系是
的位置关系是 为圆心的圆与直线
为圆心的圆与直线 相切.
相切. 的方程;
的方程; 、
、 ,圆内动点
,圆内动点 满足
满足 ,求
,求 的取值范围.
的取值范围.