题目内容
已知函数 (
( 且
且 )
)
(1)若函数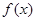 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值;
(2)将函数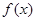 图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数
图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数 的图象,写函数
的图象,写函数 的解析式;
的解析式;
(3)若(2)中平移后所得的函数 的图象不经过第二象限,求
的图象不经过第二象限,求 的取值范围.
的取值范围.
 (
( 且
且 )
)(1)若函数
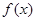 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值;(2)将函数
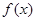 图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数
图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数 的图象,写函数
的图象,写函数 的解析式;
的解析式;(3)若(2)中平移后所得的函数
 的图象不经过第二象限,求
的图象不经过第二象限,求 的取值范围.
的取值范围.(1) (2)
(2) (3)
(3)
 (2)
(2) (3)
(3)
(1)因为函数 在
在 上是单调函数,
上是单调函数,
所以
所以 …………………………………………6分
…………………………………………6分
(2)依题意,所得函数 ………………8分
………………8分
(3)由 函数图象恒过
函数图象恒过 点,且不经过第二象限,
点,且不经过第二象限,
可得 ,即
,即 ,
,
解得 .
.
所以 的取值范围是
的取值范围是 ………………………………12分
………………………………12分
 在
在 上是单调函数,
上是单调函数, 所以

所以
 …………………………………………6分
…………………………………………6分(2)依题意,所得函数
 ………………8分
………………8分(3)由
 函数图象恒过
函数图象恒过 点,且不经过第二象限,
点,且不经过第二象限, 可得
 ,即
,即 ,
,解得
 .
. 所以
 的取值范围是
的取值范围是 ………………………………12分
………………………………12分
练习册系列答案
相关题目
 满足,
满足, 时,
时, 。
。 时,
时, 上递减。
上递减。 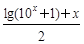 ,h (x)=
,h (x)=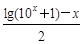
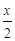 ,h (x)=lg(10x+1)-
,h (x)=lg(10x+1)- 上的函数
上的函数 满足
满足 .当
.当 时,
时, ,当
,当 时,
时, 。则
。则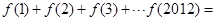 ( )
( ) 是偶函数,且在
是偶函数,且在 上是增加的。(12分)
上是增加的。(12分) 存在整数零点,则m的取值集合为 .
存在整数零点,则m的取值集合为 . ,
, ,1.5634="5.968" ).
,1.5634="5.968" ). 的大小关系是____________________
的大小关系是____________________ 。
。