题目内容
已知实数x,y满足lg(x+1),lg(2y),lg[4(x-1)]成等差数列,求点M(x,y)的轨迹方程.
答案:
解析:
解析:
|
解:由题意可得:2lg(2y)=lg(x+1)+lg[4(x-1)]. 即lg(2y)2=lg[4(x+1)(x-1)], 化简得x2-y2=1 又x-1>0,y>0,所以点M的轨迹方程为 x2-y2=1(x>1,y>0). |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤. 则z=2x-y的取值范围( )
则z=2x-y的取值范围( )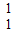 ],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.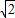 sin(
sin(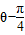 ),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为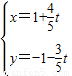 (t为参数),求直线l被曲线C所截得的弦长.
(t为参数),求直线l被曲线C所截得的弦长.
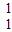 ],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
],并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.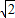 sin(
sin(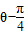 ),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
),以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为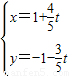 (t为参数),求直线l被曲线C所截得的弦长.
(t为参数),求直线l被曲线C所截得的弦长.