题目内容
(本小题满分14分)如图所示,在四棱锥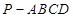 中,
中,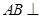 平面
平面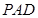 ,
,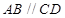 ,
,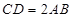 ,
,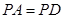 ,
,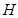 是
是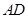 的中点.
的中点.
(1)证明: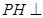 平面
平面 ;
;
(2)若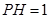 ,
,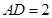 ,
, ,求二面角
,求二面角 的正切值.
的正切值.
解:(1)证明:∵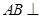 平面
平面 ,∴
,∴ 。
。
∵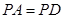 ,
,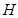 是
是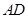 的中点
的中点
∴ 为△
为△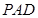 中
中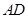 边上的高,
边上的高,
∴ 。
。
∵ ,
,
∴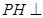 平面
平面 。……………………6分
。……………………6分
(2)方法1:延长DA、CB相交于点F,连接PF、DB
过点P作PE⊥BC,垂足为E,连接HE
由(1)知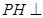 平面
平面 ,则PH⊥BC
,则PH⊥BC
又∵PE∩PH=P,∴BC⊥平面PHE,∴BC⊥HE
∴∠PEH就是所求二面角P-BC-D的平面角……………9分
在△FDC中,∵PH=1,AD=1,∴PD=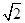
∵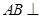 平面
平面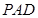 ,
,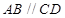 ,∴CD⊥平面PAD
,∴CD⊥平面PAD
∴CD⊥PD,∵PC= ,∴CD=4
,∴CD=4
∵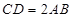 ,∴AB=2,∴BD=
,∴AB=2,∴BD=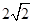 ,
,
∴AB是△FCD的中位线,FD=CD
∴BD⊥CF
∴HE=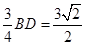
∵PH=1,∴ ……………14分
……………14分
方法2:由(1)知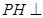 平面
平面 ,如图建立空间直角坐标系.
,如图建立空间直角坐标系.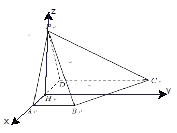
∵PH=1,AD=1,∴PD=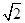
∵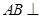 平面
平面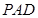 ,
,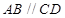 ,∴CD⊥平面PAD
,∴CD⊥平面PAD
∴CD⊥PD,∵PC= ,∴CD=4
,∴CD=4
∴
设平面BCD、平面PBC的法向量分别为
则 ,设
,设
∵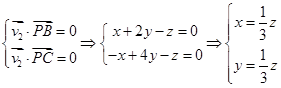 ,令
,令 ,则
,则
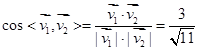 ,设二面角P-BC-D为
,设二面角P-BC-D为 ,
,
则 ,故
,故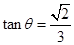
解析

练习册系列答案
相关题目
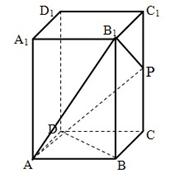
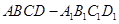 中,
中,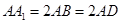 ,且
,且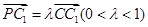 .
.
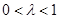 ,总有
,总有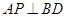 ;
;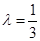 ,求二面角
,求二面角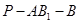 的余弦值;
的余弦值;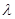 ,使得
,使得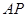 在平面
在平面 上的射影平分
上的射影平分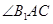 ?若存在, 求出
?若存在, 求出 ,
, ,E为棱
,E为棱 的中点.
的中点. ; (Ⅱ) 求证:
; (Ⅱ) 求证: 平面
平面 ;
; 的体积.
的体积.
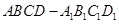 中,底面
中,底面 是边长为
是边长为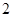 的正方形,
的正方形,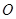 为
为 与
与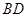 的交点,
的交点,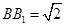 ,
,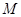 是线段
是线段 的中点.
的中点.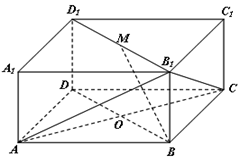
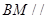 平面
平面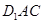 ;
;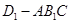 的体积
的体积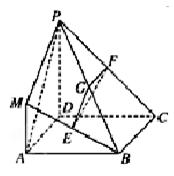
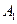 点,且
点,且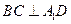 ;
;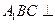 平面
平面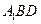 ;
;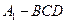 的体积.
的体积. 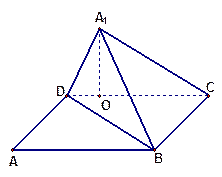
 满分14分)
满分14分)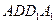 中,点
中,点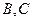 在线
在线 段
段 上,且
上,且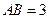 ,
,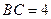 ,作
,作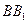 //
//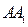 ,分别交
,分别交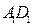 ,
,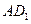 于点
于点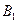 ,
,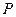 ,作
,作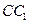 //
//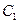 ,
,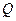 ,将该正方形沿
,将该正方形沿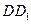 与
与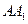 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱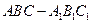 .
.
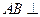 平面
平面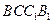 ;
;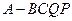 的体积;
的体积;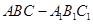 中,
中,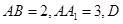 为
为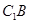
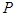 为
为 边上的动点.
边上的动点.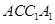 ;
;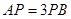 ,求三棱锥
,求三棱锥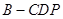 的体积.
的体积.