题目内容
如图,在长方体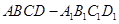 中,
中,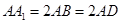 ,且
,且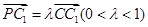 .
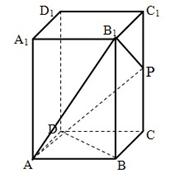
.
(I)求证:对任意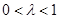 ,总有
,总有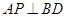 ;
;
(II)若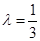 ,求二面角
,求二面角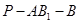 的余弦值;
的余弦值;
(III)是否存在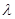 ,使得
,使得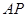 在平面
在平面 上的射影平分
上的射影平分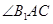 ?若存在, 求出
?若存在, 求出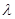 的值, 若不存在,说明理由.
的值, 若不存在,说明理由.
(I)见解析(II)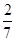 (III)存在
(III)存在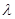
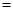

解析试题分析:(I)以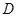 为坐标原点,分别以
为坐标原点,分别以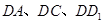 所在直线为
所在直线为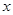 轴,
轴,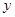 轴,
轴,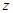 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设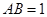 ,则
,则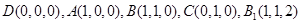 ,
,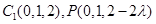 ,从而
,从而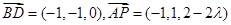 ,
,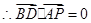 ,即
,即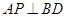 . ……4分
. ……4分
(II)由(I)及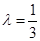 得,
得,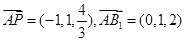 ,
,
设平面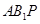 的法向量为
的法向量为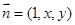 ,则
,则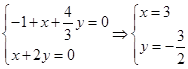 ,
,
从而可取平面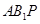 的法向量为
的法向量为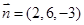 ,
,
又取平面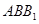 的法向量为
的法向量为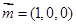 ,且设二面角
,且设二面角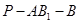 为
为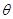 ,
,
所以 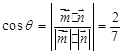 ……8分
……8分
(III) 假设存在实数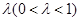 满足条件,由题结合图形,只需满足
满足条件,由题结合图形,只需满足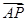 分别与
分别与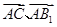 所成的角相等,
所成的角相等,
即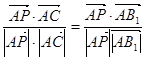 ,即
,即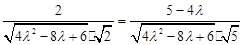 ,
,
解得 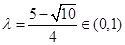 .
.
所以存在满足题意得实数 ,
,
使得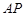 在平面
在平面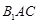 上的射影平分
上的射影平分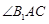 . ……12分
. ……12分
考点:本小题主要考查长方体中的线线垂直的证明、二面角的求法及综合应用问题,考查学生的空间想象能力和利用空间向量解决立体几何问题的能力,考查学生的空间想象能力和运算求解能力以及分析问题解决问题的能力.
点评:立体几何问题可以转化为用空间向量来解决,可以省去作二面角、线面角等步骤之间求解,但是求解时一定要注意运算的准确性.

练习册系列答案
相关题目
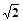 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。
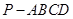 中,底面
中,底面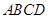 为平行四边形,
为平行四边形,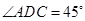 ,
,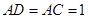 ,
,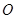 为
为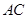 中点,
中点,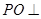 平面
平面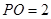 ,
,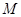 为
为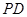 中点.
中点.
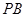 //平面
//平面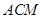 ;
; 平面
平面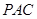 ;
;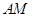 与平面
与平面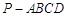 中
中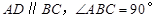 ,
, 平面
平面 ,
,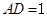 ,
,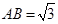 ,
,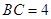 .
.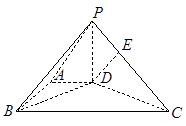
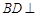
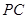 ;
;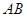 与平面
与平面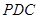 所成的角;
所成的角;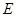 在棱
在棱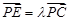 ,若
,若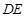 ∥平面
∥平面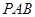 ,求
,求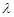 的值.
的值.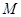 、
、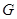 分别是
分别是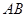 、
、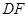 的中点.
的中点.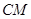
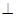 平面
平面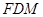
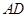 上(含
上(含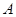 、
、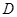 端点)确定一点
端点)确定一点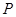 ,使得
,使得
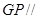 平面
平面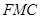 ,并给出证明;
,并给出证明;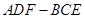 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体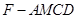 内的概率.
内的概率. 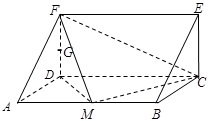
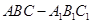 的各棱长均为2,侧面
的各棱长均为2,侧面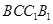
 底面
底面 ,侧棱
,侧棱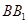 与底面
与底面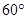 .
.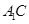 与底面
与底面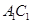 上是否存在点
上是否存在点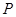 ,使得平面
,使得平面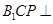 平面
平面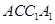 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。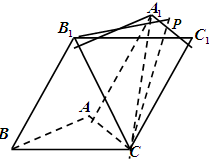
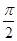 ,AB=BC=2AD=4,
,AB=BC=2AD=4,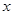 ,G是BC的中点.
,G是BC的中点.
 ,求
,求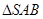 与直角梯形
与直角梯形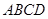 垂直,
垂直,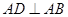 ,
,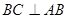 ,
,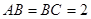 ,
,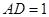 .若
.若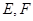 分别为
分别为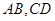 的中点.
的中点.
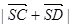 的值; (2)求面
的值; (2)求面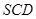 与面
与面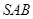 所成的二面角大小.
所成的二面角大小.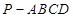 中,
中,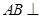 平面
平面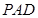 ,
,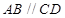 ,
,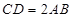 ,
,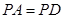 ,
,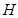 是
是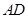 的中点.
的中点.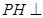 平面
平面 ;
;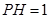 ,
,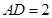 ,
, ,求二面角
,求二面角 的正切值.
的正切值.