题目内容
观察按下列顺序排列的等式: ,
, ,
, ,
, ,…,猜想第
,…,猜想第 个等式应为( )
个等式应为( )
A. | B. |
C. | D. |
B
解析试题分析:先观察已知等式的左边,可得第 个等式的左边应为:
个等式的左边应为: ;再观察已知等式的右边结果:1、11、21、31、…知它们构成以1为首项,10为公差的等差数列,所以第
;再观察已知等式的右边结果:1、11、21、31、…知它们构成以1为首项,10为公差的等差数列,所以第 个等式的右边应为:
个等式的右边应为: ;故选B
;故选B
考点:归纳猜想.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
有一段演绎推理是这样的:“直线平行于平面,则此直线平行于平面内的所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 平面
平面 ,则直线
,则直线 直线
直线 ”结论显然是错误的,这是因为( )
”结论显然是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
下列正确的是( )
| A.类比推理是由特殊到一般的推理 |
| B.演绎推理是由特殊到一般的推理 |
| C.归纳推理是由个别到一般的推理 |
| D.合情推理可以作为证明的步骤 |
下面使用的类比推理中恰当的是( )
A.“若 ,则 ,则 ”类比得出“若 ”类比得出“若 ,则 ,则 ” ” |
B.“ ”类比得出“ ”类比得出“ ” ” |
C.“ ”类比得出“ ”类比得出“ ” ” |
D.“ ”类比得出“ ”类比得出“ ” ” |
根据给出的数塔猜测123 456×9+7= ( )
1×9+2=11
12×9+3=111
123×9+4=1 111
1 234×9+5=11 111
12 345×9+6=111 111
……
| A.1 111 110 | B.1 111 111 |
| C.1 111 112 | D.1 111 113 |
用火柴棒摆“金鱼”,如图所示: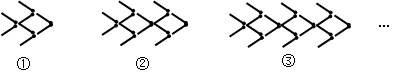
按照上面的规律,第4个“金鱼”图需要火柴棒的根数为
| A.24 | B.26 | C.28 | D.30 |
用演绎法证明函数 是增函数时的小前提是
是增函数时的小前提是
| A.增函数的定义 |
B.函数 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则 |
D.若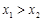 ,则 ,则 |
如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…),
则在第n个图形中共有( )个顶点。
| A.(n+1)(n+2) | B.(n+2)(n+3) | C. +3n+8 +3n+8 | D.12n |
 ,则输出的数是 .
,则输出的数是 .