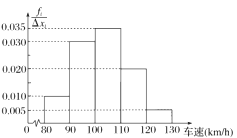
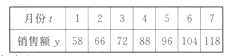
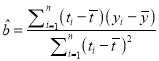题目内容
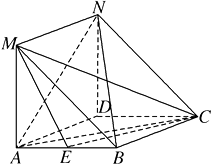
【题目】一张坐标纸上涂着圆E： 
及点P（1，0），折叠此纸片，使P与圆周上某点P'重合，每次折叠都会留下折痕，设折痕与直线EP'交于点M ．
（1）求 
的轨迹 
的方程；
（2）直线 
与C的两个不同交点为A ， B ， 且l与以EP为直径的圆相切，若 
，求△ABO的面积的取值范围．
【答案】
（1）解：折痕为PP′的垂直平分线，则|MP|=|MP′|，由题意知圆E的半径为2 
，
∴|ME|+|MP|=|ME|+|MP′|=2 ＞|EP|，
∴E的轨迹是以E、P为焦点的椭圆，且a= ，c=1，
∴b2=a2﹣c2=1， ∴M的轨迹C的方程为 
（2）解：l与以EP为直径的圆x2+y2=1相切，
则O到l即直线AB的距离： 
=1，即m2=k2+1，
由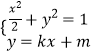 
，消去y ， 得（1+2k2）x2+4kmx+2m2﹣2=0，
∵直线l与椭圆交于两个不同点，
∴△=16k2m2﹣8（1+2k2）（m2﹣1）=8k2＞0，k2＞0，
设A（x1 ， y1），B（x2 ， y2），则 
， 
，
y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2= 
，
又 
=x1x2+y1y2= ，∴ 
，∴ 
，
= 
= 
，
设μ=k4+k2 ， 则 
，∴ 
= 
， 
，
∵S△AOB关于μ在[ 
，2]单调递增，
∴ 
，∴△AOB的面积的取值范围是[ 
， 
]
【解析】本题主要考查圆锥曲线的综合应用和平面向量的数量积的问题。第一小题主要考查圆锥曲线的轨迹方程的问题，根据已知条件中的垂直平分线，根据垂直平分线的特点，可以得到动点到两定点的和为定值，可以得出轨迹为椭圆，根据椭圆的特点确定a,b,c即可。第二小题主要考查直线与圆锥曲线的综合应用的问题，要求三角形的面积，就要先找到底和高，由已知条件可知，高是确定的1，所以求底也就是要求弦长的问题，也就要联立直线和椭圆方程，然后利用韦达定理和向量的数量积进行求解弦长AB即可。
