题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{f(x-4),x>2}\\{{e}^{x},-2≤x≤2}\\{f(-x),x<-2}\end{array}\right.$,则f(-2017)=e.分析 由已知得f(-2017)=f(2017)=f(504×4+1)=f(1),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{f(x-4),x>2}\\{{e}^{x},-2≤x≤2}\\{f(-x),x<-2}\end{array}\right.$,
∴f(-2017)=f(2017)=f(504×4+1)=f(1)=e1=e.
故答案为:e.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
12.为弘扬中国传统文化,某校在高中三个年级中抽取甲、乙、丙三名同学进行问卷调查.调查结果显示这三名同学来自不同的年级,加入了不同的三个社团:“楹联社”、“书法社”、“汉服社”,还满足如下条件:
(1)甲同学没有加入“楹联社”;
(2)乙同学没有加入“汉服社”;
(3)加入“楹联社”的那名同学不在高二年级;
(4)加入“汉服社”的那名同学在高一年级;
(5)乙同学不在高三年级.
试问:丙同学所在的社团是( )
(1)甲同学没有加入“楹联社”;
(2)乙同学没有加入“汉服社”;
(3)加入“楹联社”的那名同学不在高二年级;
(4)加入“汉服社”的那名同学在高一年级;
(5)乙同学不在高三年级.
试问:丙同学所在的社团是( )
| A. | 楹联社 | B. | 书法社 | ||
| C. | 汉服社 | D. | 条件不足无法判断 |
16.若点P是以F1,F2为焦点的双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)上一点,PF1⊥PF2,且|PF1|=2|PF2|,则此双曲线的标准方程是( )
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | x2-$\frac{{y}^{2}}{5}$=1 | D. | x2-$\frac{{y}^{2}}{6}$=1 |
10.曲线y=$\frac{2}{x}$与直线y=x-1及x=1所围成的封闭图形的面积为( )
| A. | 2-ln2 | B. | 2ln2-$\frac{1}{2}$ | C. | 2+ln2 | D. | 2ln2+$\frac{1}{2}$ |
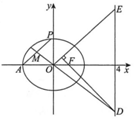 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3. 在平面直角坐标系xOy中,圆C的方程是x2+y2=4.
在平面直角坐标系xOy中,圆C的方程是x2+y2=4.