题目内容
在正三角形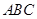 中,
中,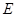 、
、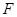 、
、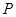 分别是
分别是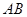 、
、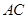 、
、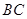 边上的点,满足
边上的点,满足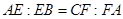
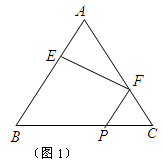
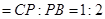 (如图1).将△
(如图1).将△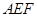 沿
沿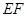 折起到
折起到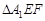 的位置,使二面角
的位置,使二面角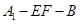 成直二面角,连结
成直二面角,连结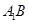 、
、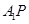 (如图2)
(如图2)
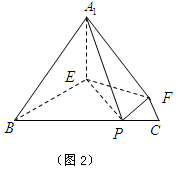
(Ⅰ)求证: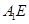 ⊥平面
⊥平面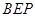 ;
;
(Ⅱ)求二面角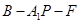 的余弦值.
的余弦值.
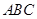 中,
中,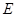 、
、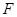 、
、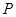 分别是
分别是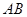 、
、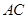 、
、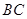 边上的点,满足
边上的点,满足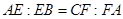
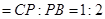 (如图1).将△
(如图1).将△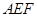 沿
沿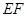 折起到
折起到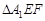 的位置,使二面角
的位置,使二面角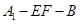 成直二面角,连结
成直二面角,连结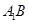 、
、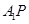 (如图2)
(如图2)

(Ⅰ)求证:
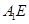 ⊥平面
⊥平面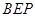 ;
;(Ⅱ)求二面角
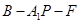 的余弦值.
的余弦值.(Ⅰ)取BE的中点D,连结DF∵AE EB=CF
EB=CF FA=1
FA=1 2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,AE=DE=1,∴EF⊥AD,在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.∴A1E⊥BE∴A1E⊥平面BEF,即A1E⊥平面BEP(Ⅱ)
2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,AE=DE=1,∴EF⊥AD,在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.∴A1E⊥BE∴A1E⊥平面BEF,即A1E⊥平面BEP(Ⅱ)
 EB=CF
EB=CF FA=1
FA=1 2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,AE=DE=1,∴EF⊥AD,在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.∴A1E⊥BE∴A1E⊥平面BEF,即A1E⊥平面BEP(Ⅱ)
2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,AE=DE=1,∴EF⊥AD,在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.∴A1E⊥BE∴A1E⊥平面BEF,即A1E⊥平面BEP(Ⅱ)
试题分析:不妨设正三角形ABC 的边长为 3 .

(I)在图1中,取BE的中点D,连结DF.
∵AE
 EB=CF
EB=CF FA=1
FA=1 2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,
2,∴AF=AD=2,而∠A=600,∴△ADF是正三角形,又AE=DE=1,∴EF⊥AD. 2分
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,∴A1E⊥BE.
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP. .4分
(II)建立分别以ED、EF、EA为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A(0,0,1),
B(2,0,0),F(0,
 ,0), P (1,
,0), P (1,  ,0),则,
,0),则, .
.设平面ABP的法向量为
 ,
, 由
 平面ABP知,
平面ABP知, ,即
,即 令
令 ,得
,得 ,
, .
. ,设平面AFP的法向量为
,设平面AFP的法向量为 .
.由
 平面AFP知,
平面AFP知, ,即
,即 令
令 ,得
,得 ,
, .
. ,
,所以二面角B-A1P-F的余弦值是
 13分
13分点评:证明线面垂直主要通过已知中的垂直的直线来推理,其重要注意翻折前后保持不变的量;第二问二面角的求解充分把握好从点E出发的三线两两垂直建立空间坐标系,通过两面的法向量的夹角得到二面角

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 中,侧棱
中,侧棱 底面
底面 ,
,

 平面
平面
 与平面
与平面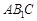 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值 ,写出
,写出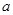 、
、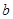 是两条不同的直线,
是两条不同的直线,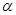 、
、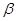 是两个不同的平面,则下列正确的个数为:( )
是两个不同的平面,则下列正确的个数为:( )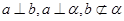 ,则
,则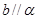 ; ②若
; ②若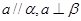 ,则
,则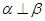 ;
;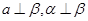 ,则
,则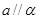 或
或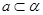 ;④若
;④若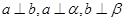 ,则
,则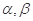 是两个不同的平面,则下列四个命题中是真命题的是( )
是两个不同的平面,则下列四个命题中是真命题的是( )



 ,其边长为2,
,其边长为2,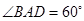 ,
,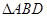 绕着
绕着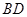 顺时针旋转
顺时针旋转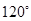 得到
得到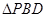 ,
,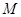 是
是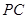 的中点.
的中点.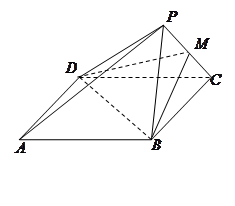
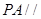 平面
平面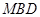 ;
;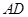 与平面
与平面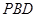 所成角的正弦值.
所成角的正弦值.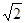 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.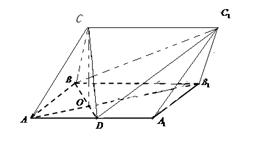
 内(含正方体表面)任取一点
内(含正方体表面)任取一点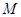 ,则
,则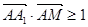 的概率
的概率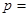 ( )
( ) 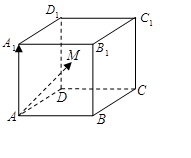




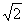 .
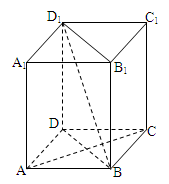
.
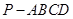 中,
中,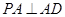 ,
,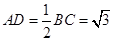 ,
,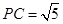 .
.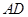 ∥
∥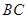 ,
,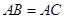 .
.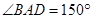
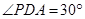 .
.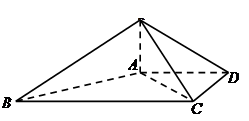
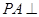 平面
平面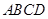 ;
;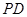 上是否存在一点
上是否存在一点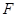 ,使直线
,使直线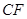 与平面
与平面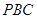 成角正弦值等于
成角正弦值等于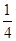 ,若存在,指出
,若存在,指出