题目内容
对于n∈N*,将n表示为n= +…+
+…+ ,当i=k时,ai=1,当0≤i≤k-1时,ai为0或1.定义bn如下:在n的上述表示中,当a,a1,a2,…,ak中等于1的个数为奇数时,bn=1;否则bn=0.
,当i=k时,ai=1,当0≤i≤k-1时,ai为0或1.定义bn如下:在n的上述表示中,当a,a1,a2,…,ak中等于1的个数为奇数时,bn=1;否则bn=0.(1)b2+b4+b6+b8= ;
(2)记cm为数列{bn}中第m个为0的项与第m+1个为0的项之间的项数,则cm的最大值是 .
【答案】分析:(1)由题设定义可知,2=1×2,4=1×22,6=1×22+1×2,8=1×23,从而b2=1,b4=1,b6=0,b8=1,故可求b2+b4+b6+b8的值;
(2)设{bn}中第m个为0的项为bi,即bi=0,构造二进制数(i)10=(akak-1…a1a)2,则akak-1…a1a中1的个数为偶数,再进行分类讨论:当a2a1a=000时,cm=2;当a2a1a=001时,cm=0;当a2a1a=010时,cm=1;当a2a1a=011时,cm=0;当a2a1a=100时,cm=2;当a2a1a=101时,cm=0;当a=0,前面有奇数个1时,cm=1; 当a=0,前面有偶数个1时,cm=2;当末位有奇数个1时,cm=1;当末位有偶数个1时,cm=0,由此可得cm的最大值.
解答:解:(1)由题设定义可知,2=1×2,4=1×22,6=1×22+1×2,8=1×23,∴b2=1,b4=1,b6=0,b8=1
∴b2+b4+b6+b8=3
(2)设{bn}中第m个为0的项为bi,即bi=0,构造二进制数(i)10=(akak-1…a1a)2,则akak-1…a1a中1的个数为偶数,当a2a1a=000时,bi+1=1,bi+2=1,bi+3=0,cm=2;
当a2a1a=001时,bi+1=0,cm=0;当a2a1a=010时,bi+1=1,bi+2=0,cm=1;当a2a1a=011时,bi+1=0,cm=0;当a2a1a=100时,bi+1=1,bi+2=1,bi+3=0,cm=2;当a2a1a=101时,bi+1=0,cm=0;当a=0,前面有奇数个1时,bi+1=1,bi+2=0,cm=1; 当a=0,前面有偶数个1时,bi+1=1,bi+2=1,bi+3=0,cm=2;当末位有奇数个1时,bi+1=1,bi+2=0,cm=1;当末位有偶数个1时,bi+1=1,bi+2=0,cm=0;故cm的最大值为2.
点评:对于新定义型问题,正确理解新定义传递的信息是解题的突破口.
(2)设{bn}中第m个为0的项为bi,即bi=0,构造二进制数(i)10=(akak-1…a1a)2,则akak-1…a1a中1的个数为偶数,再进行分类讨论:当a2a1a=000时,cm=2;当a2a1a=001时,cm=0;当a2a1a=010时,cm=1;当a2a1a=011时,cm=0;当a2a1a=100时,cm=2;当a2a1a=101时,cm=0;当a=0,前面有奇数个1时,cm=1; 当a=0,前面有偶数个1时,cm=2;当末位有奇数个1时,cm=1;当末位有偶数个1时,cm=0,由此可得cm的最大值.
解答:解:(1)由题设定义可知,2=1×2,4=1×22,6=1×22+1×2,8=1×23,∴b2=1,b4=1,b6=0,b8=1
∴b2+b4+b6+b8=3
(2)设{bn}中第m个为0的项为bi,即bi=0,构造二进制数(i)10=(akak-1…a1a)2,则akak-1…a1a中1的个数为偶数,当a2a1a=000时,bi+1=1,bi+2=1,bi+3=0,cm=2;
当a2a1a=001时,bi+1=0,cm=0;当a2a1a=010时,bi+1=1,bi+2=0,cm=1;当a2a1a=011时,bi+1=0,cm=0;当a2a1a=100时,bi+1=1,bi+2=1,bi+3=0,cm=2;当a2a1a=101时,bi+1=0,cm=0;当a=0,前面有奇数个1时,bi+1=1,bi+2=0,cm=1; 当a=0,前面有偶数个1时,bi+1=1,bi+2=1,bi+3=0,cm=2;当末位有奇数个1时,bi+1=1,bi+2=0,cm=1;当末位有偶数个1时,bi+1=1,bi+2=0,cm=0;故cm的最大值为2.
点评:对于新定义型问题,正确理解新定义传递的信息是解题的突破口.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
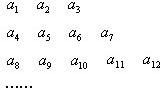 将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: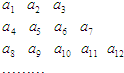 将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知:
将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知: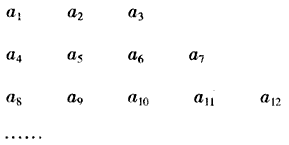
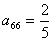 ,请解答以下问题:
,请解答以下问题: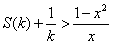 在
在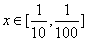 上有解,求正整数k的取值范围。
上有解,求正整数k的取值范围。