题目内容
证明f(x)=
思路分析:可采用定义法和求导法两种方法来解题,体会求导法在解决函数单调性问题上的优越性.
证明:法一:任取两个数x1,x2∈(0,+∞),设x1<x2,则
f(x1)-f(x2)=![]() -
-![]() =
=![]() ,
,
∵x1>0,x2>0且x1<x2,∴f(x1)-f(x2)>0.∴f(x1)>f(x2).
∴f(x)在(0,+∞)上是减函数.
法二:f′(x)=![]() ,
,
∵x>0,∴f′(x)<0.
∴f(x)在(0,+∞)上是减函数.
辨析比较 比较一下两种方法,用求导证明更简捷一些.如果是更复杂的函数,用导数的符号判断函数的单调性更能显示出它的优越性.

练习册系列答案
相关题目
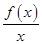 .
. 在(-∞,0)上的增减性.
在(-∞,0)上的增减性. sin 2x),函数f(x)=p·q-5(a∈R,a≠0)
sin 2x),函数f(x)=p·q-5(a∈R,a≠0)