题目内容
已知函数f(x)的导函数为f ′(x)，且对任意x＞0，都有f ′(x)＞
．
（Ⅰ）判断函数F(x)＝在(0，＋∞)上的单调性；
（Ⅱ）设x1，x2∈(0，＋∞)，证明：f(x1)＋f(x2)＜f(x1＋x2)；
（Ⅲ）请将（Ⅱ）中的结论推广到一般形式，并证明你所推广的结论．
解：（Ⅰ）对F(x)求导数，得F′(x)＝
．
∵f ′(x)＞，x＞0，∴xf ′(x)＞f(x)，即xf ′(x)－f(x)＞0，
∴F′(x)＞0．
故F(x)＝在(0，＋∞)上是增函数．……………………………………………4分
（Ⅱ）∵x1＞0，x2＞0，∴0＜x1＜x1＋x2．
由（Ⅰ），知F(x)＝在(0，＋∞)上是增函数，
∴F(x1)＜F(x1＋x2)，即
＜
．
∵x1＞0，∴f(x1)＜
f(x1＋x2)．
同理可得f(x2)＜
f(x1＋x2)．
以上两式相加，得f(x1)＋f(x2)＜f(x1＋x2)．………………………………………8分
（Ⅲ）（Ⅱ）中结论的推广形式为：
设x1，x2，…，xn∈(0，＋∞)，其中n≥2，则f(x1)＋f(x2)＋…＋f(xn)＜f(x1＋x2＋…＋xn)．
∵x1＞0，x2＞0，…，xn＞0，
∴0＜x1＜x1＋x2＋…＋xn．
由（Ⅰ），知F(x)＝在(0，＋∞)上是增函数，
∴F(x1)＜F(x1＋x2＋…＋xn)，即＜
．
∵x1＞0，
∴f(x1)＜
f(x1＋x2＋…＋xn)．
同理可得
f(x2)＜
f(x1＋x2＋…＋xn)，
f(x3)＜
f(x1＋x2＋…＋xn)，
……
f(xn)＜
f(x1＋x2＋…＋xn)．
以上n个不等式相加，得f(x1)＋f(x2)＋…＋f(xn)＜f(x1＋x2＋…＋xn)．………14分
练习册系列答案
手拉手全优练考卷系列答案
相关题目
的图象如图所示，那么函数f (x)的图象最有可能的是( )
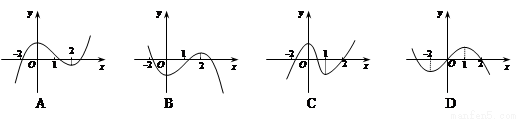
，且满足f(x)＝2x
＋ln x，则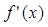
的图像如左图所示，那么函数f(x)的图像最有可能的