题目内容
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,且
平面ABCD,且![]() ,
,![]() .四边形ABCD满足
.四边形ABCD满足![]() ,
,![]() ,
,![]() .E为侧棱PB的中点,F为侧棱PC上的任意一点.
.E为侧棱PB的中点,F为侧棱PC上的任意一点.

(1)若F为PC的中点,求证:![]() 平面PAD;
平面PAD;
(2)求证:平面![]() 平面PAB;
平面PAB;
(3)是否存在点F,使得直线AF与平面PCD垂直?若存在,写出证明过程并求出线段PF的长;若不存在,请说明理由.
【答案】(1)见解析;(2)见解析;(3)存在,![]()
【解析】
(1)易得![]() ,利用线面平行的判定证明;
,利用线面平行的判定证明;
(2)易得AD⊥平面PAB,利用面面垂直的判定,可得AD平面AFD,所以平面AFD⊥平面PAB;
(3)易得CD⊥平面PAC.只需在棱PC上存在点F使得AF⊥PC即可.
(1)因为E,F分别为侧棱PB,PC的中点,
所以![]() ,因为
,因为![]() ,
,
所以![]() ,而
,而![]() 平面PAD,
平面PAD,![]() 平面PAD,
平面PAD,
所以![]() 平面PAD;
平面PAD;
(2)因为平面![]() 平面PAC,平面
平面PAC,平面![]() 平面
平面![]() ,
,
且![]() ,
,![]() 平面PAC,
平面PAC,
所以![]() 平面ABCD,又
平面ABCD,又![]() 平面ABCD,所以
平面ABCD,所以![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() 平面PAB,
平面PAB,
而![]() 平面AFD,所以平面
平面AFD,所以平面![]() 平面PAB;
平面PAB;
(3)在棱PC上显然存在点F使得![]() .
.
由已知,![]() ,
,![]() ,
,![]() ,
,![]() .
.
由平面几何知识可得![]() .
.
由(2)知,![]() 平面ABCD,所以
平面ABCD,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面PAC.
平面PAC.
而![]() 平面PAC,所以
平面PAC,所以![]() .
.
又因为![]() ,所以
,所以![]() 平面PCD.
平面PCD.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
可求得,![]() ,
,![]() .
.
可见直线![]() 与平面PCD能够垂直,此时线段PF的长为
与平面PCD能够垂直,此时线段PF的长为![]() .
.

【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.
【题目】为了推行“智慧课堂”教学,某老师分别用传统教学和“智慧课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期屮考试后,分别从两个班级屮各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
乙班频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以上统计数据填写下面![]() 列联表,并判断“成绩优良与教学方式是否有关”?
列联表,并判断“成绩优良与教学方式是否有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
| p>成绩不优良 | |||
总计 |
附: 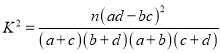 .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)现从上述40人中,学校按成绩是否优良采川分层扣样的方法扣取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.