题目内容
已知函数 (
( 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)已知函数 在
在 处取得极小值,不等式
处取得极小值,不等式 的解集为
的解集为 ,若
,若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
解:(Ⅰ)当 时,
时, ,
, ,
, ,得
,得 ,
,
所以曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(Ⅱ) .
.
当 时,
时, 恒成立,此时
恒成立,此时 的单调递增区间为
的单调递增区间为 ,无单调递减区间;
,无单调递减区间;
当 时,
时, 时,
时, ,
, 时,
时, ,
,
此时 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为
(Ⅲ)由题意知 得
得 ,经检验此时
,经检验此时 在
在 处取得极小值.
处取得极小值.
因为 ,所以
,所以 在
在 上有解,即
上有解,即 使
使 成立,…9分
成立,…9分
即 使
使 成立,
成立,
所以 .
.
令 ,
, ,所以
,所以 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
则 ,
,
所以 .
.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在边长为 的正方形
的正方形 中任取一点
中任取一点 ,则点
,则点 恰好落在正方形与曲线
恰好落在正方形与曲线 围成的区域内(阴影部分)的概率为( )
围成的区域内(阴影部分)的概率为( )
| A. | B. |
| C. | D. |
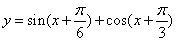 的最大值是
的最大值是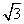 (D)
(D)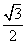
 是抛物线
是抛物线 :
: 的焦点,则
的焦点,则 _______.
_______. 



 的焦点为
的焦点为 ,准线为直线
,准线为直线 ,过抛物线上一点
,过抛物线上一点 于
于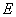 ,若直线
,若直线 的倾斜角为
的倾斜角为 ,则
,则 ______.
______.  (B)
(B) (C)
(C) (D)
(D)


 ,
, ,
,  ,
, 中为偶函数的是
中为偶函数的是 ,且
,且 的解集为
的解集为 .
. 的值;
的值; 都是正数,且
都是正数,且 ,求证:
,求证: