题目内容
cos（-2040°）=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：原式先利用偶函数的性质化简，角度变形后利用诱导公式计算即可得到结果．
解答：
解：原式=cos2040°=cos（6×360°-120°）=cos120°=-
，
故选：B．
| 1 |
| 2 |
故选：B．
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
已知复数z=1-i（其中i为虚数单位），则
等于（ ）
| 2i |
| z |
| A、1-i | B、1+i |
| C、-1-i | D、-1+i |
复数z=
的共轭复数是（ ）
| -3+i |
| 2+i |
| A、-1-i | B、2-i |
| C、-1+i | D、2+i |
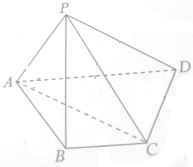如图四棱锥P-ABCD的底面是梯形，BC∥AD，AB=BC=CD=1，AD=2，平面PAC⊥平面ABCD．