题目内容
下列各组向量中,可以作为基底的是( )
A. | B. |
C. | D. |
C
解析试题分析:根据题意,对于选项A,由于零向量与任何向量共线,不能作为基底,对于B,由于 ,共线,故不成立,对于C,
,共线,故不成立,对于C,  ,故成立,对于选项D,由于
,故成立,对于选项D,由于 ,由于
,由于 ,可知共线,故选C.
,可知共线,故选C.
考点:平面向量的基本定理
点评:解决的关键是根据平面向量的基底的定义来判定,不共线的向量即可,属于基础题。

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
设 ,向量
,向量 且
且 ,则
,则 ( )
( )
A. | B. | C. | D. |
设 ,
, ,
, 为坐标平面上三点,
为坐标平面上三点, 为坐标原点,若
为坐标原点,若 与
与 在
在 方向上的投影相同,则
方向上的投影相同,则 与
与 满足的关系式为( )
满足的关系式为( )
A. | B. | C. | D. |
以下说法错误的是 ( )
A.直角坐标平面内直线的倾斜角的取值范围是 |
B.直角坐标平面内两条直线夹角的取值范围是 |
C.平面内两个非零向量的夹角的取值范围是 |
D.空间两条直线所成角的取值范围是 |
若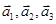 均为单位向量,则“
均为单位向量,则“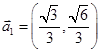 ”是“
”是“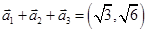 ”的(
”的( 条件。
条件。
| A.充分非必要 | B.必要非充分 | C.既不充分也不必要 | D.充要 |
 ,且
,且 ,则
,则 或
或
 ,则
,则 或
或 ,满足
,满足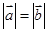 ,则
,则
 与
与 平行,则
平行,则 其中真命题的个数是
其中真命题的个数是 B.
B. C.
C. D.
D.
 、
、 分别为
分别为 ,则
,则 =( )
=( ) B.
B.  C.
C.  D.
D. 

 ,
,
 ,
,
 ,则①
,则①
 ,②
,②
 ,③
,③
 ,④
,④ 中正确的等式的个数为 ( )
中正确的等式的个数为 ( )






