题目内容
某实验室一天的温度(单位: )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系; .
.
(1)求实验室这一天上午8时的温度;
(2)求实验室这一天的最大温差.
(1)10 ;(2)4
;(2)4 .
.
解析试题分析:(1)把 中的自变量
中的自变量 用8代替计算即可;(2)利用两个角的和的正弦公式把
用8代替计算即可;(2)利用两个角的和的正弦公式把 变成
变成 ,根据
,根据 求出
求出 的取值范围,确定
的取值范围,确定 的取值范围,从而求得
的取值范围,从而求得 在
在 上的最大值与最小值,最大值减去最小值即得最大温差.
上的最大值与最小值,最大值减去最小值即得最大温差.
(1)

 .
.
故实验室上午8时的温度为10 .
.
(2)因为 ,
,
又 ,所以
,所以 ,
, .
.
当 时,
时, ;当
;当 时,
时, .
.
于是 在
在 上取得最大值12,取得最小值8.
上取得最大值12,取得最小值8.
故实验室这一天最高温度为12 ,最低温度为8
,最低温度为8 ,最大温差为4
,最大温差为4 .
.
考点:三角函数的实际运用,两个角的和的正弦公式,三角函数的最值.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 (
( ,
, )为偶函数,其图象上相邻的两个对称轴之间的距离为
)为偶函数,其图象上相邻的两个对称轴之间的距离为 .
. 的解析式;
的解析式; ,求
,求 的值.
的值. .
. 的单调递增区间;
的单调递增区间; 是
是 的三个内角,且
的三个内角,且 ,
, ,又
,又 ,求
,求 边的长.
边的长. ,
, ,且
,且 .
. 的值;
的值; ,
, ,求
,求 .
. (sin2x-cos2x)-2sinxcosx.
(sin2x-cos2x)-2sinxcosx. ,
,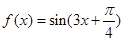 .
. 的单调递增区间;
的单调递增区间;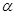 是第二象限角,
是第二象限角, ,求
,求 的值.
的值. .
. ,
, ,且C为锐角,求
,且C为锐角,求 .
. .
.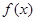 的值域;
的值域; 的内角
的内角 的对边长分别为
的对边长分别为 ,若
,若 ,
, ,求
,求 的值.
的值.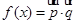 ,而
,而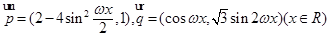 .
.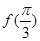 最大,求
最大,求 能取到的最小正数值.
能取到的最小正数值.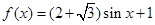 且
且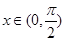 ,求
,求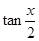 .
.