题目内容
已知双曲线的实轴平行于y轴,离心率为2,它的一个分支过圆(x-1)2+(y-1)2=4的中心,且此分支一侧的焦点在这个圆上,求这个分支顶点的轨迹方程.
答案:
解析:
解析:
如图所示,圆心(1,1)在双曲线上,它到焦点(在圆上)的距离为2,又它的离心率为2,∴ 圆心到准线的距离等于1 ∴ 准线为y=2或y=0,设顶点P(x,y)
(1)当y=0作准线时, 又这点在圆上 (2)当y=2作准线时, 又这点在圆上 ∴ 所求的轨迹方程为(x-1)2+(3y-1)2=4 (y>0), 或(x-1)2+(3y-5)2=4(y<2 |

练习册系列答案
相关题目

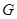 的中心在原点,它的渐近线与圆
的中心在原点,它的渐近线与圆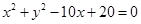 相切. 过点
相切. 过点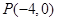 作斜率为
作斜率为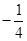 的直线
的直线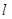 ,使
,使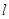 和
和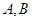 两点,和
两点,和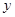 轴交于
轴交于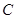 点,且点
点,且点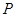 在线段
在线段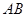 上,满足
上,满足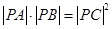
 的中心在原点,它的短轴是
的中心在原点,它的短轴是