题目内容
16．函数f（x）=$\frac{{x}^{2}}{2}$+ax+2lnx，（a∈R）在x=2处取得极值．（Ⅰ）求实数a的值及函数f（x）单调区间；
（Ⅱ）方程f（x）=m有三个实数x1，x2，x3（x1＜x2＜x3），求证：x3-x1＜2．
分析 （1）求导，在x=2处取得极值，可得f′（2）=2+a+1=0，利用导数求单调区间；
（2）利用导数求出原函数的单调区间和极值，模拟函数图象；方程f（x）=m有三个实数x1，x2，x3（x1＜x2＜x3），等价于函数y=f（x）与直线y=m有三个交点，
根据函数图象得出x的范围．
解答 解：（1）f′（x）=x+a+$\frac{2}{x}$，
∵在x=2处取得极值，
∴f′（2）=2+a+1=0，
∴a=-3，
∴f′（x）=x-3+$\frac{2}{x}$=$\frac{（x-2）（x-1）}{x}$，
当x∈（0，1）和（2，+∞）时，f′（x）＞0，f（x）递增，
当x∈（1，2）时，f′（x）＜0，f（x）递减；
（2）由（1）可知：f（1）=$\frac{5}{2}$是函数f（x）的极大值；f（2）=ln4-4是函数f（x）的极小值，
∵方程f（x）=m有三个实数x1，x2，x3（x1＜x2＜x3）；
∴函数y=f（x）与直线y=m有三个交点，
画出函数y=f（x）与y=m的图象，如图所示：
由图可知：ln4-4＜m＜$\frac{5}{2}$；则$\frac{1}{2}$＜x1＜1；2＜x3＜$\frac{5}{2}$
∴x3-x1＜$\frac{5}{2}$-$\frac{1}{2}$=2．
点评 考察了极值点的概念，利用导函数求单调区间和极值并模拟函数图象，利用图象法证明问题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
6．已知集合P={x|x2-x-2≤0}，Q={x|log2（x-1）≤1}，则P∩Q=（ ）
| A． | （-1，3） | B． | [-1，3） | C． | （1，2] | D． | [1，2] |
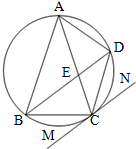如图，四边形ABCD内接于圆，AB=AC，直线MN切圆于点C，BD∥MN交AC于点E．若AB=6，BC=4，则AE的长为$\frac{10}{3}$．
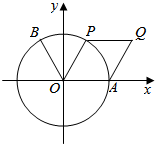如图，点B（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），点A时单位圆与x轴正半轴的交点．设点P为单位圆上的动点，点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$，∠AOP=2θ（$\frac{π}{6}$≤θ＜$\frac{π}{2}$），f（θ）=$\overrightarrow{OB}$•$\overrightarrow{OQ}$，求f（θ）的取值范围，当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时，求四边形OAQP的面积．
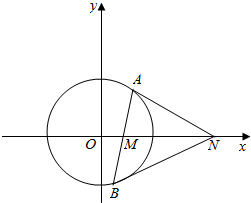如图，已知圆O：x2+y2=r2（r＞0），动直线l过点M（1，0）交圆O于A（x1，y1），B（x2，y2）两点（点A在x轴上方），点N在x轴上，若点B的坐标为（0，-r），则点A的横坐标为$\frac{8}{5}$．