Question

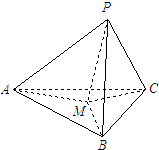（2010•广东模拟）如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f(M)=(

1

2

，x，y)，则x+y=

1

2

．

Answer 1

分析：先根据三棱锥的特点求出其体积，然后利用新定义通过体积，推出建立x与y的关系，解之即可．

解答：解：∵PA、PB、PC两两垂直，且PA=3．PB=2，PC=1．
∴V _P-ABC=

1

3

×

1

2

×3×2×1=1=

1

2

+x+y
即x+y=

1

2

故答案为：

1

2

．

点评：本题主要考查了棱锥的体积，同时考查了基本不等式的运用，是题意新颖的一道题目，属于中档题．