题目内容
如图,四边形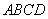 为矩形,
为矩形,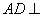 平面
平面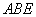 ,
, ,
,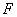 为
为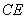 上的点,且
上的点,且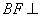 平面
平面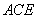 .
.
(1)求证: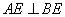 ;
;
(2)设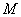 在线段
在线段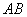 上,且满足
上,且满足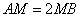 ,试
,试
在线段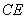 上确定一点
上确定一点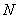 ,使得
,使得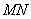 ∥平面
∥平面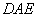 .
.

(1)证明 ∵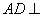 平面
平面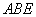 ,
, ∥
∥ ,
,
 ∴
∴ ⊥平面
⊥平面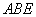 ,
,
∵ 平面
平面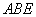 ,∴
,∴ .
.
又∵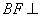 平面
平面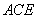 ,
, 平面
平面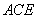 ,
,
∴ ,
,
∵ ,∴
,∴ 平面
平面 ,
,
又∵ 平面
平面 ,∴
,∴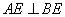 .
.
(2) 当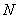 点为线段
点为线段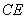 上靠近
上靠近 点的一个三等分点时,
点的一个三等分点时,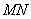 ∥平面
∥平面 。证明如下
。证明如下
在 中,过
中,过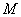 点作
点作 ∥
∥ 交
交 于
于 点.
点.
在 中,过
中,过 点作
点作 ∥
∥ 交
交 于
于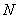 点,连接
点,连接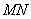 .
.
 则由比例关系易得
则由比例关系易得 .
.
∵ ∥
∥ ,
,
 平面
平面 ,
, 平面
平面 ,
,
∴ ∥平面
∥平面 .
.
同理, ∥平面
∥平面 .
.
∵ ,
,
∴平面 ∥平面
∥平面 .
.
而 平面
平面 ,∴
,∴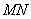 ∥平面
∥平面 .
.
∴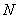 点为线段
点为线段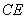 上靠近
上靠近 点的一个三等分点.
点的一个三等分点.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 和共面的直线
和共面的直线 ,
, ,下列命题是真命题的是( )
,下列命题是真命题的是( ) B.若
B.若 ,
, ,则
,则 ,
, ,则
,则 ,则
,则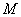 ,
,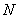 分别是
分别是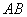 ,
,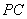 的中点。求证:
的中点。求证: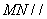 平面
平面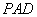 ;(要求用线面平行的判定定理与面面平行的性质定理两种方法证明)
;(要求用线面平行的判定定理与面面平行的性质定理两种方法证明)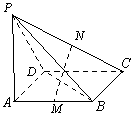
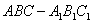 中,侧面
中,侧面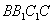 为菱形,
为菱形,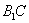 的中点为
的中点为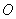 ,且
,且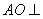 平面
平面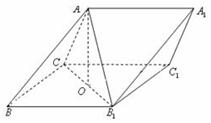
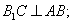
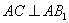 ,
,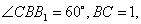 求三棱柱
求三棱柱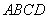 的边长为
的边长为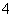 ,
,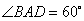 ,
,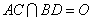 .将菱形
.将菱形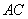 折起,得到三棱锥
折起,得到三棱锥 ,点
,点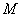 是棱
是棱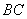 的中点,
的中点, .
.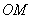 ∥平面
∥平面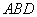 ;
;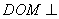 平面
平面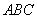 ;
;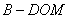 的体积.
的体积.
 为直线,
为直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
, ,则
,则 B.若
B.若 ,
, ,则
,则 ,
, ,若
,若 ,则
,则 ( )
( ) .
.
 .
.
 .
.
 .
.
