题目内容
已知圆的极坐标方程为ρ=2cosθ,则该圆的圆心到直线ρsinθ+2ρcosθ=1的距离是分析:先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,将极坐标方程为ρ=2cosθ和ρsinθ+2ρcosθ=1化成直角坐标方程,最后利用直角坐标方程的形式,结合点到直线的距离公式求解即得.
解答:解:由ρ=2cosθ,化为直角坐标方程为x2+y2-2x=0,其圆心是A(1,0),
由ρsinθ+2ρcosθ=1得:
化为直角坐标方程为2x+y-1=0,
由点到直线的距离公式,得d=
=
.
故答案为
.
由ρsinθ+2ρcosθ=1得:
化为直角坐标方程为2x+y-1=0,
由点到直线的距离公式,得d=
| |2+0-1| | ||
|
| ||
| 5 |
故答案为
| ||
| 5 |
点评:本小题主要考查圆和直线的极坐标方程与直角坐标方程的互化,以及利用圆的几何性质计算圆心到直线的距等基本方法,属于基础题.

练习册系列答案
相关题目
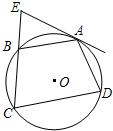 A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.